검색결과 리스트
글
이 번에는 선형시스템의 정의를 한번 살펴보고 간단한 미분 방정식의 해법을 한 번 알아보도록 하겠습니다. |
Linearity 선형성
어떤 시스템이 선형이라는 것은 Superposition이 만족해야합니다. Superposition이라는 것은
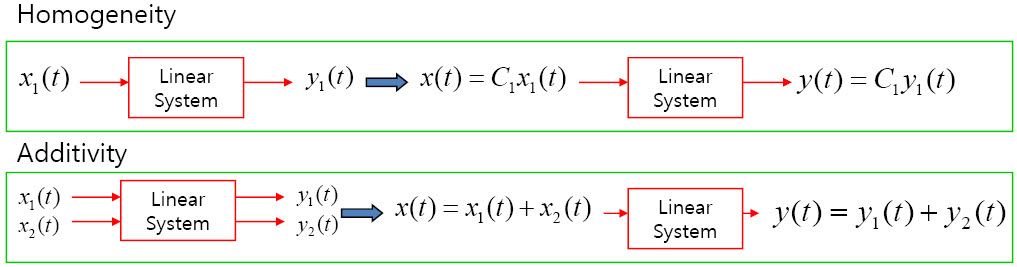
위의 Homogeneity와 Additivity가 동시에 만족해야하는 데요. Homogeneity는 어떤 입력에 대한 출력을 가지는 시스템이 그 입력에 상수배를 하면 출력도 그대로 상수배로 나타난다는 것이구요. Additivity는 각각 다른 두 입력에 대한 두 출력이, 그 두 입력을 더해서 입력하면 출력도 더해져서 나타난다는 것입니다. 위 두 성질을 한번에 쓰면
Superposition이라고 하며 위와 같이 설명할 수 있습니다.
LTI 시스템 : Linear Time Invariant System
어떤 시스템이 LTI 시스템이라고 하면, 위에서 설명한 선형(Linear)의 성질을 가지면서 추가로 Time Invariant 시불변성을 가져야합니다.
어떤 입력에 대한 출력은 시간이 흘러도 변하지 않아야한다는 것이지요. 선형시불변성의 의미입니다.
미분방정식의 종류
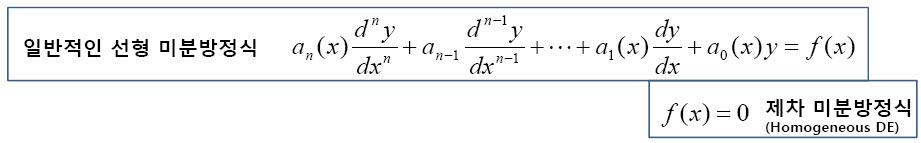
변수 분리형 미분방정시
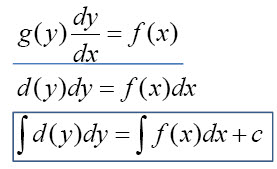
위에 보이는 형태의 비방은 변수분리형으로서 그 해법은 보다시피 정형화되어있습니다.
Homogeneous Linear Equations
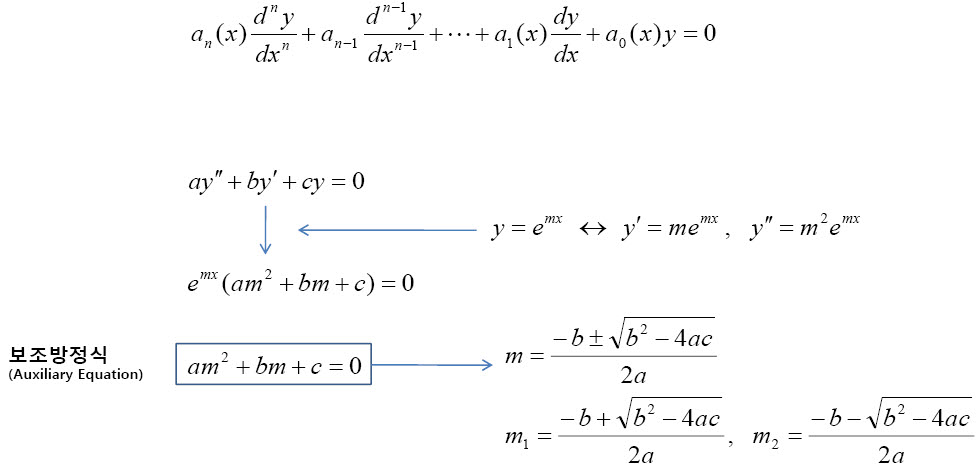
위의 제차방정식은 보조방정식을 이용해서 간단히 해법을 찾을 수 있습니다.
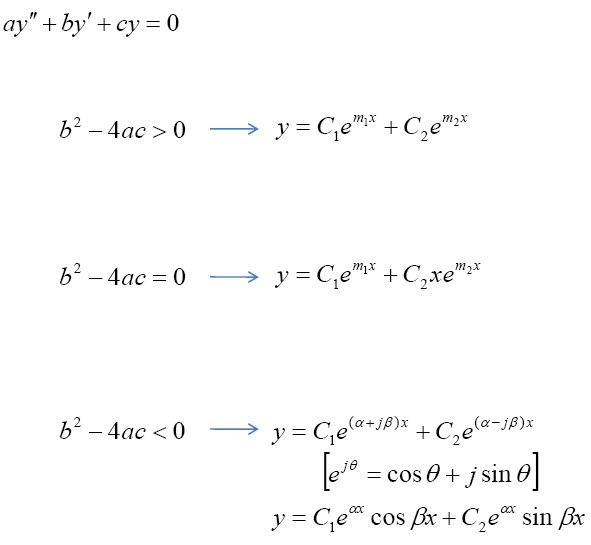
만약 2차미분방정식이라면 위와같이 보조방정식이 2차식이 되어 중고등학교때 배운 근의 공식으로 간단히 그 결과를 얻을 수 있는데요. 조심해야할것은 서로다른 두 실근, 중근, 허근... 등의 상황에 따라 해법이 달라진다는 것에 주의해야합니다.
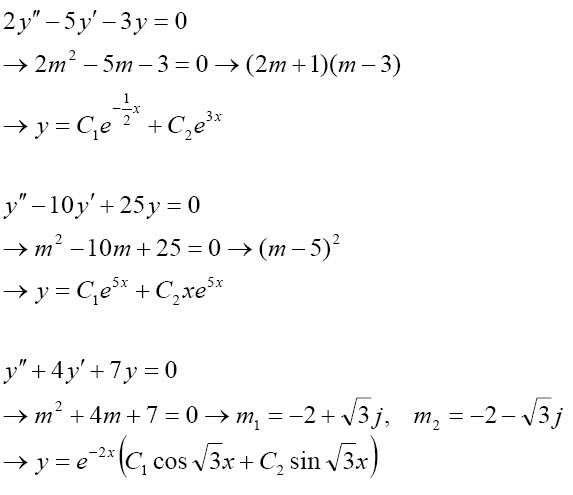
위에 간단한 예제를 들어두었습니다.
Continuous System.pdf'The Robot > Theory' 카테고리의 다른 글
| [공업수학] 벡터의 외적 (8) | 2009/08/30 |
|---|---|
| [공업수학] 벡터의 내적 (2) | 2009/08/30 |
| [공업수학] 벡터의 기초 (4) | 2009/08/30 |
| [선형변환] Convolution 컨볼루션 적분 (6) | 2009/08/30 |
| [선형변환] Continuos Systems (4) | 2009/08/30 |
| [선형변환] Signal and Sequence (0) | 2009/08/29 |
| [C/C++] 원시데이터 유형과 연산 (0) | 2009/08/29 |
| [공학입문설계] 공학과 공학설계의 개념 (0) | 2009/08/29 |
설정
트랙백
http://pinkwink.kr/trackback/155
지나가다 보게되었는데 natural response 구할때 보조방정식을 이용한 풀이에서 중근에 해당할때 m1=m2 이니깐 저렇게 써주신 거죠? 수고하세요~
그러게요... 아랫첨자 빼고 적을껄...ㅋㅋ
아마 당시 수식입력하다 귀찮아서 CTRL-C,V 신공을 잘못 사용한 모양입니다... 감사합니다.^^.
정말 너무너무 감사합니다 찾고잇던게 여기잇네요...ㅎ
도움이 되었다니 다행입니다^^