[공업수학] 벡터의 외적 The Robot/Theory 2009/08/30 22:16


본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보조 자료 이외의 목적이 없음을 알립니다.




벡터 외적

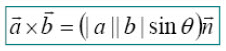
벡터의 외적의 정의입니다.

 
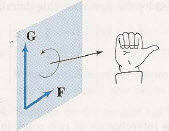
벡터 a에서 b방향으로 오른손을 감았을때 엄지손가락의 방향이 외적의 방향입니다. 내적은 스칼라값으로 나타나지만 외적은 다시 벡터의 형태로 나타난다는 것을 알아두어야합니다.

 
오른손으로 감아쥐는 방향이 중요하기 때문에 벡터의 외적은 교환법칙이 성립하지 않습니다. 물론 외적끼리의 결합법칙도 성립하지 않습니다.

 
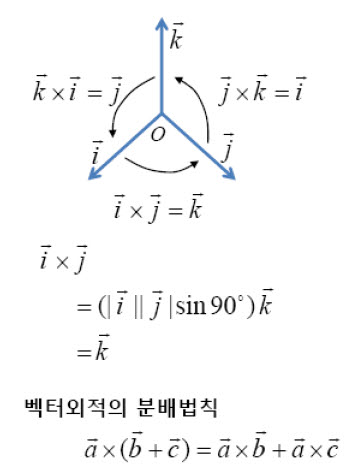
각 단위벡터들 끼리의 외적을 보여주고 있습니다. i->j->k의 순서로 흐른다는 것을 알면됩니다.

 
그래서 위 과정을 따라가면 두 벡터의 외적을 구하는 공식을 알 수 있습니다.

 

 

위에 나와 있지만, 외적의 결과가 0이면 두 벡터는 평행합니다. 


스칼라 삼중적

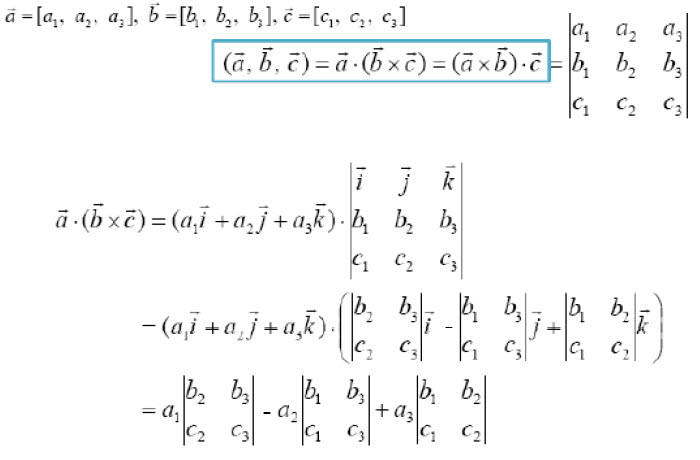
어떤 세 벡터에서 두 벡터의 외적후 나머지 한 벡터와 내적을 취하는 것을 스칼라 삼중적이라고 합니다.


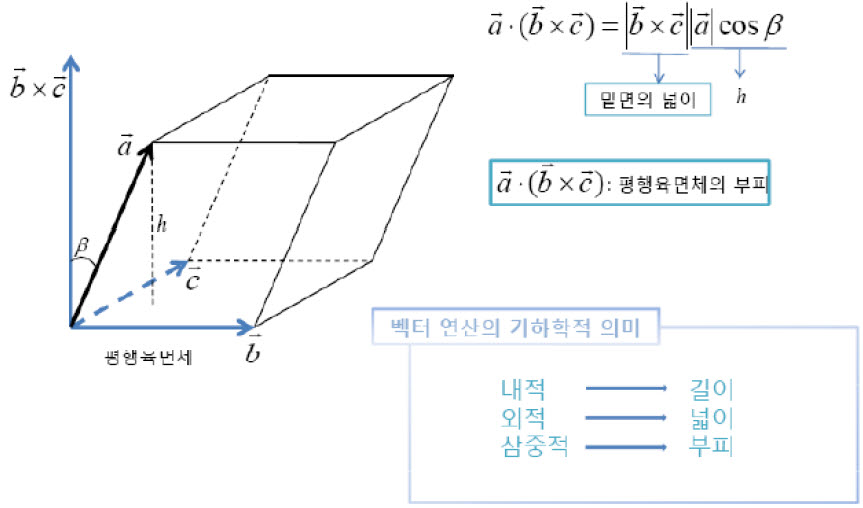
스칼라 삼중적은 평행육면체(직육면체 포함)의 부피를 의미하기도 합니다. 





참고자료:
07 Vector 04.pdf
 


'The Robot > Theory' 카테고리의 다른 글

[공학입문설계] 문제의 정의 및 공학설계 단계  (6) 2009/09/02
[공업수학] 벡터공간  (6) 2009/08/30
[공업수학] 벡터를 이용한 직선과 평면의 표현  (4) 2009/08/30
[공업수학] 벡터의 외적  (8) 2009/08/30
[공업수학] 벡터의 내적  (2) 2009/08/30
[공업수학] 벡터의 기초  (4) 2009/08/30
[선형변환] Convolution 컨볼루션 적분  (6) 2009/08/30
[선형변환] Continuos Systems  (4) 2009/08/30
,
트랙백0개 , 댓글8개
http://pinkwink.kr/trackback/159 관련글 쓰기
  • 나의별 2011/03/11 19:03

    이해하기쉽게 설명되어있네요.
    감사합니다.

  • 주입식교육 2011/04/19 17:10

    하긴 미국 유명한 서적에 그렇게 정의해서 사용하니까 그냥 외워서 쓰자라는 느김밖에는 안들어서..

    • PinkWink 2011/04/19 17:34

      또.. 약간 부족한 실력에... 교재를 따라가기 급급했다는...ㅠㅠ
      좀 더 아름다운 설명은 위키피디아를 참조하세요...

  • 우왕쩐당 2011/10/01 16:56

    유체역학 공부하는데 벡터와 내,외적이 많이 헷갈렸는데, 너무 큰 도움이 되었습니다. ^-^b 감사합니다~

    • PinkWink 2011/10/02 10:12

      네.. 다행입니다. 좋은 성과있으시길 빕니다.^^

  • 링고 2012/02/23 09:18

    오랫동안 공부를 안하다가 다시 기초공학공부 시작하고 있는데, 내용이 충실합니다. 여러모로 감사드립니다.