검색결과 리스트
글
밸런싱 로봇 만들기를 기대하시는 분들께서는 참 답답하시겠지만, 계속 동역학을 건드리고 있네요^^. 동역학모델을 익혀야하는 이유는 이야기를 했었습니다.[관련글] 그리고 그 때 소개한 동역학은 로봇의 Yaw 움직임은 고려하지 안았다고 했습니다. 그러다가 Lego사의 마인드스톰이라는 제품의 Yorihisa Yamamoto라는 분이 작성한 기술문서를 보게되어서 그 동역학의 시작을 지난 번에 소개[관련글]했었습니다.
이번에는 지난번에 이어 동역학을 정리할려고 했는데요. Lego사의 그 기술문서에서 저의 전개와 다른 것을 발견했네요. 제가 잘못했을 확률이 높습니다만, 일단, 정리를 계속하면서 어디서 차이점이 발견되었는지 이야기를 해보겠습니다.
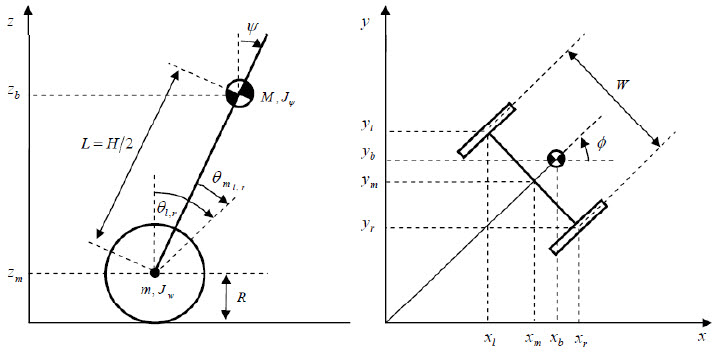
지난번에도 나왔던 그림이네요. 여기서
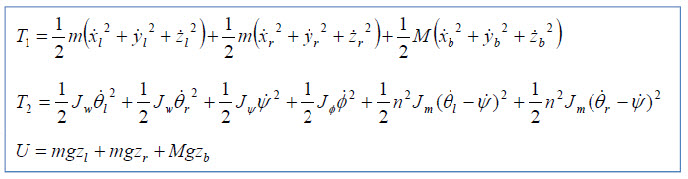
운동에너지와 위치에너지를 구한다고 했습니다. T1은 병진운동에너지 (Translation Kinetic Energy)이구요. T2는 회전운동엔너지 (Rotational Kinetic Energy)입니다. U는 위치에너지 (Potential Energy)입니다. 위 식에다가, 지난번 포스팅에서 초반에 이야기했던 위치정보들,
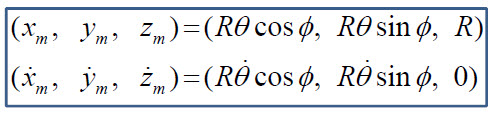
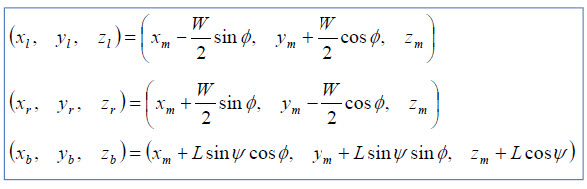
위 식들을 미분해서 대입해야합니다.
그리고 난 다음 라그랑지 방정식을 Yorihisa Yamamoto라는 분은
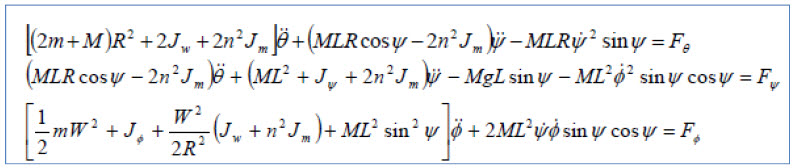
라고 소개하고 있습니다.
그런데 제가 해보니 딱 일치하지를 않았습니다. ㅠㅠ 일단 이렇게 포스팅하긴 싫었는데 말이죠. 너무 수식이 많아서 제가 전개한 부분은 그냥 스캔해서 올리겠습니다. (클릭하시면 아마 크게 나오겠죠^^)
일단, 방금 말씀드린데로. 운동에너지와 위치에너지 (T1, T2, U)들을 가지고 라그랑지안 L=T1+T2-U를 구하신 다음 상태 (theta, psi, phi)를 이용해서 라그랑지 방정식을 만드는 식은
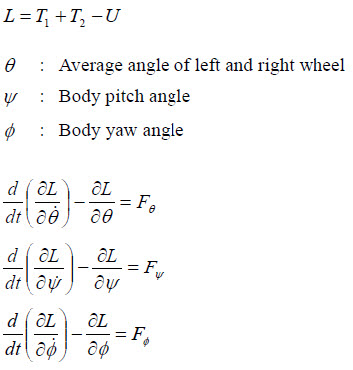
입니다. 저도 이 과정을 거쳐서 전개했습니다.
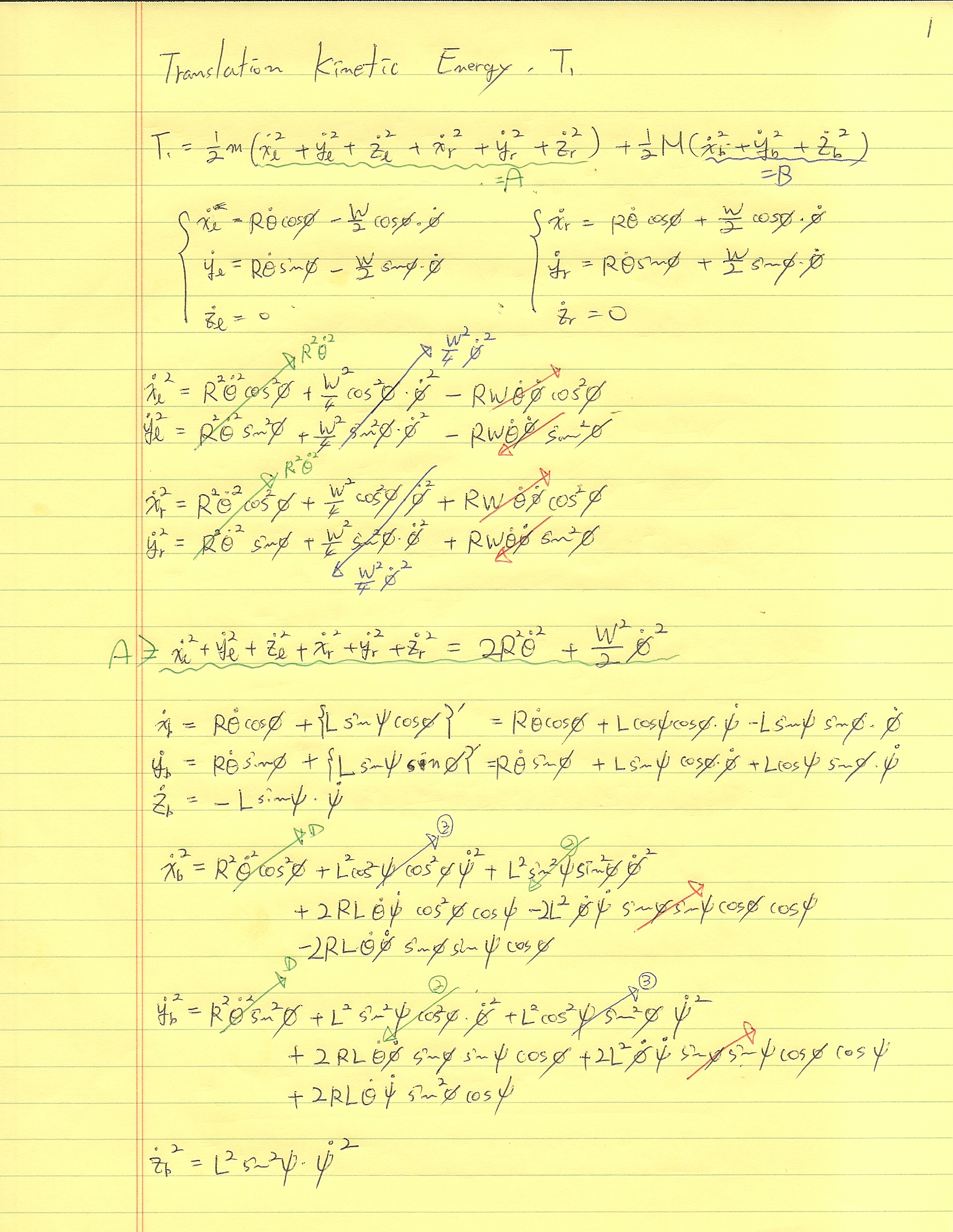
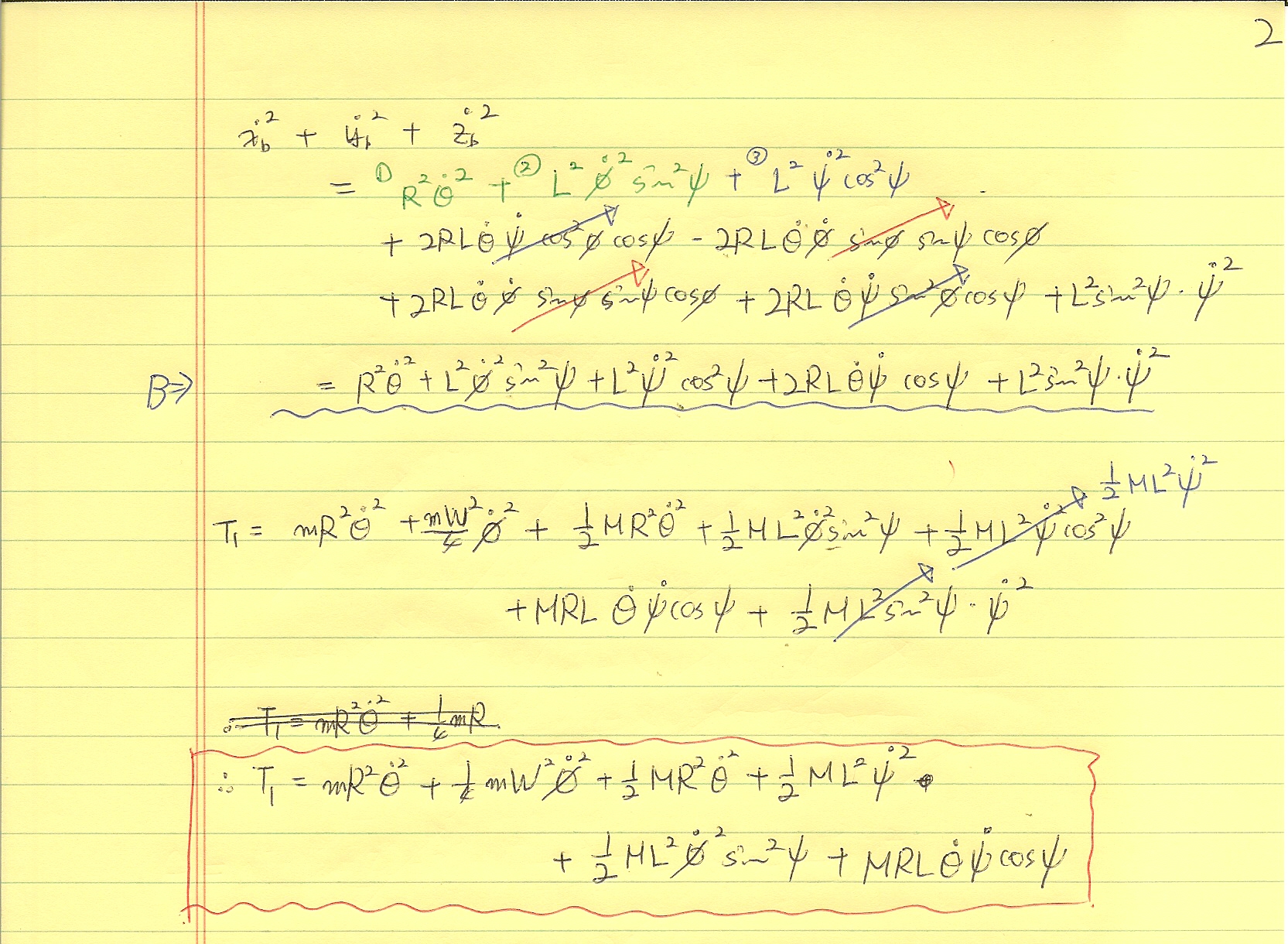
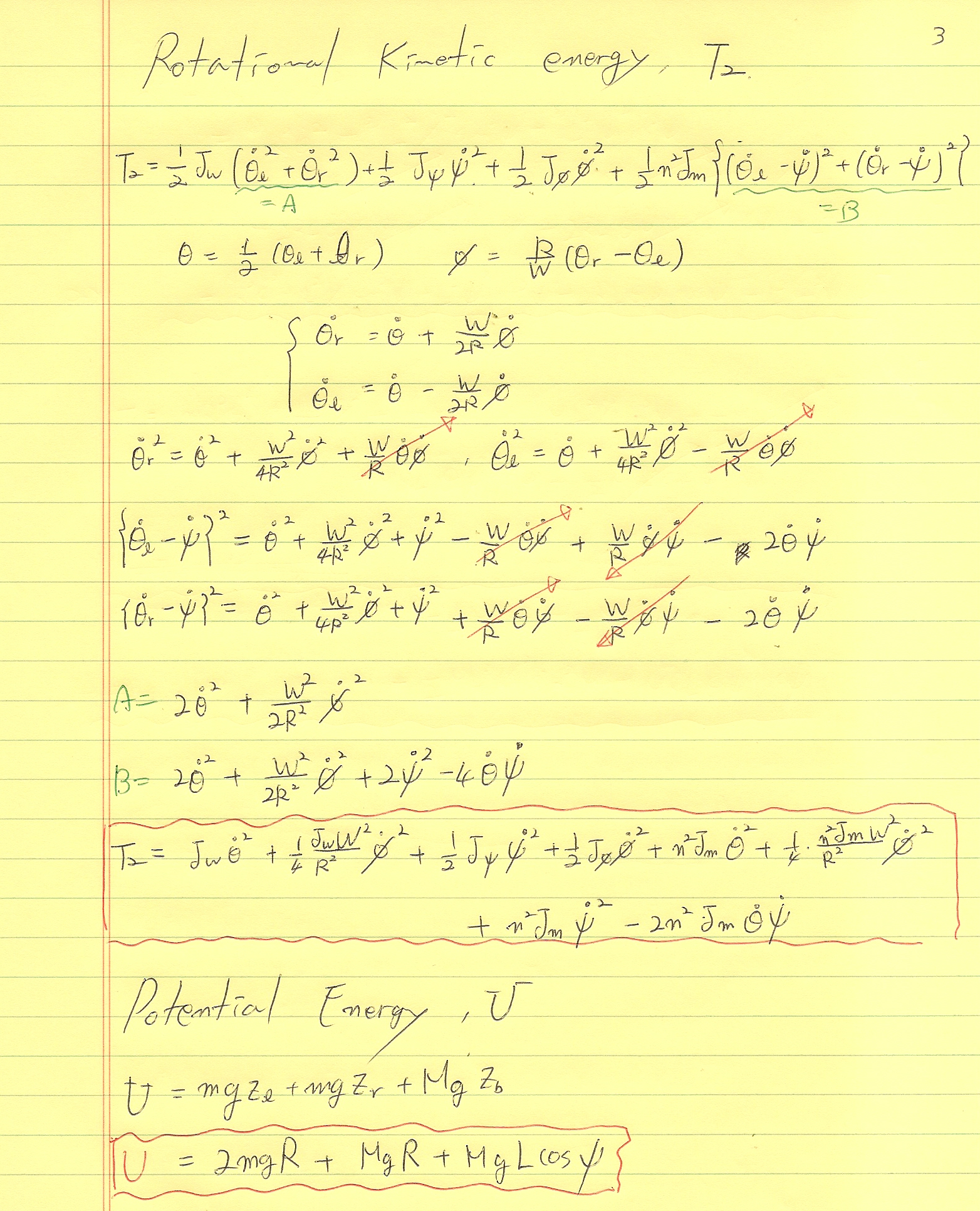
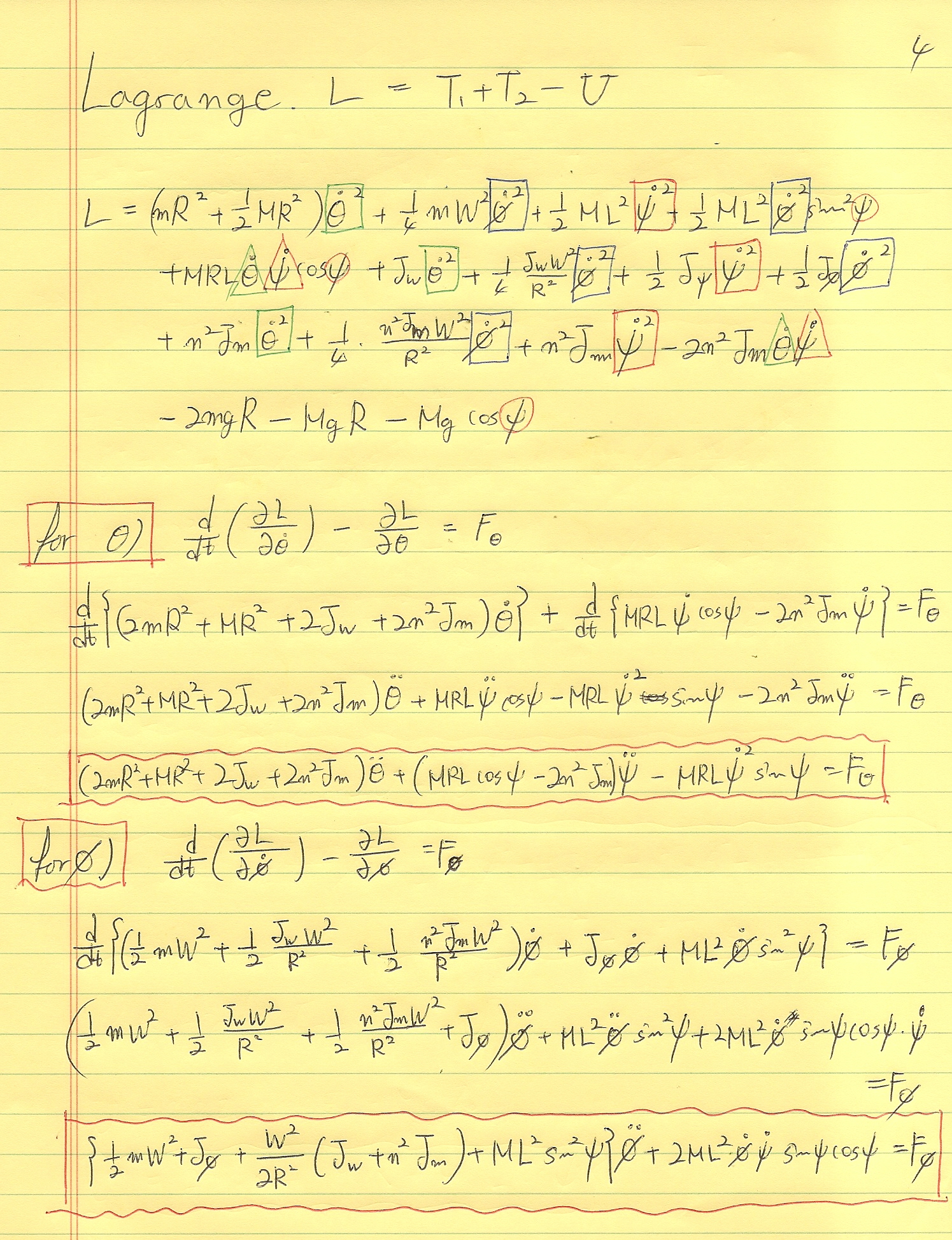
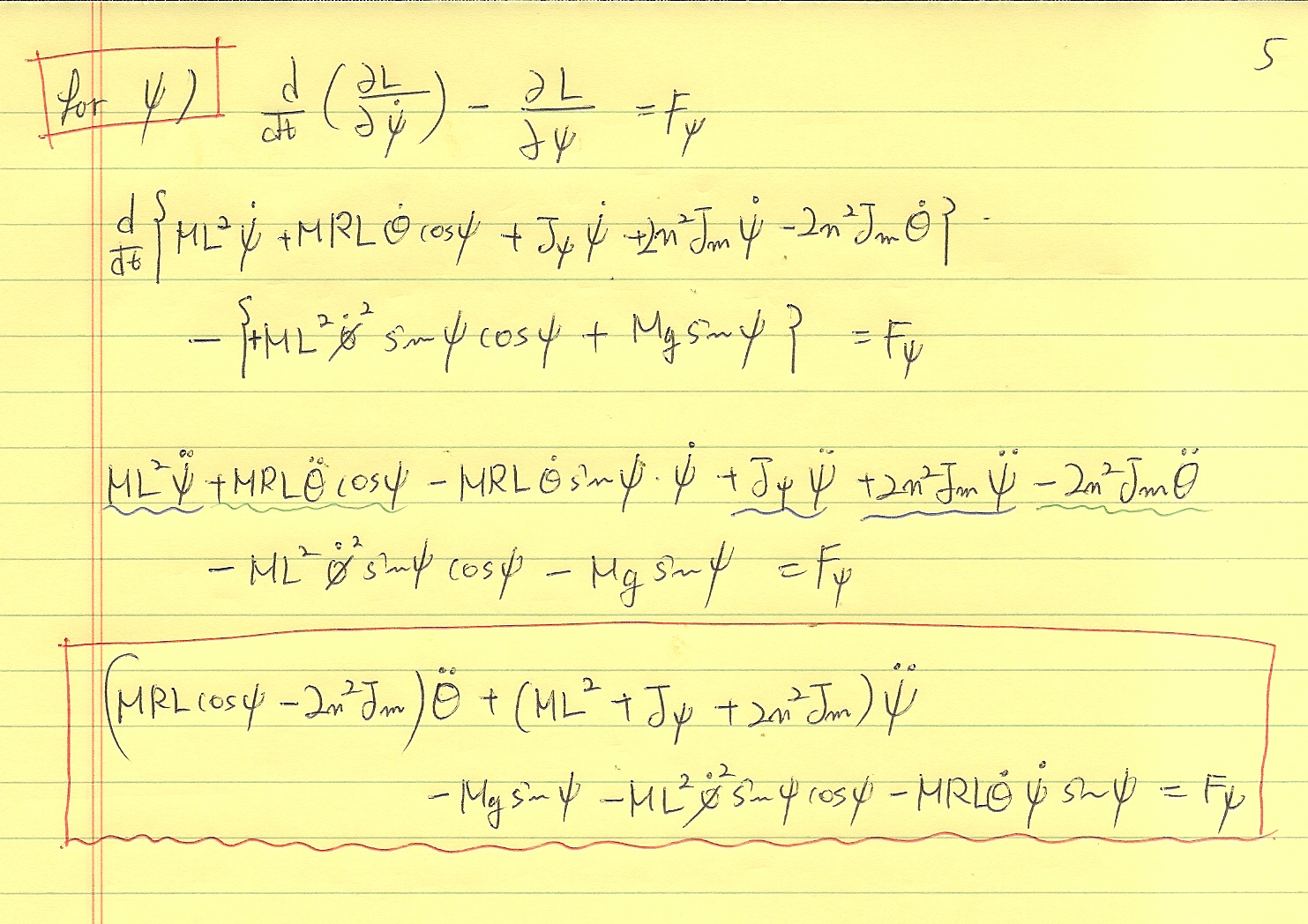
이렇게 유도를 해보았지요.ㅠㅠ. 몹쓸 글씨로 눈 아프게 해드려 죄송합니다.ㅠㅠ
|
|
|
일단 결과식을 비교해보도록 하겠습니다.
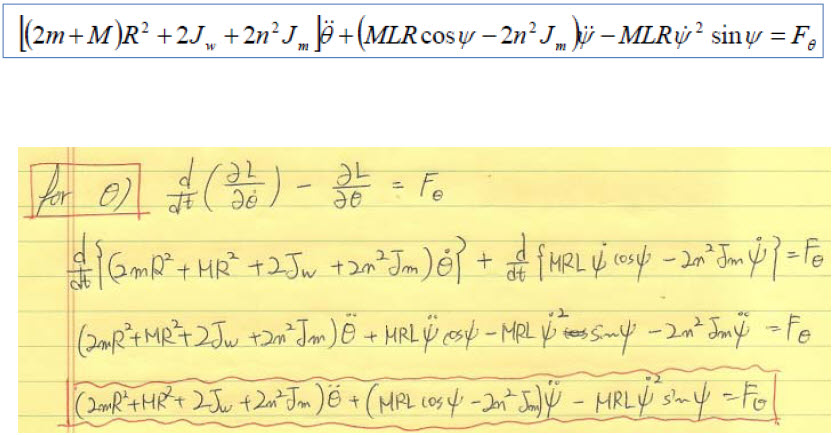
먼저 theta 상태에 대한 라그랑지 방정식은 일치합니다.
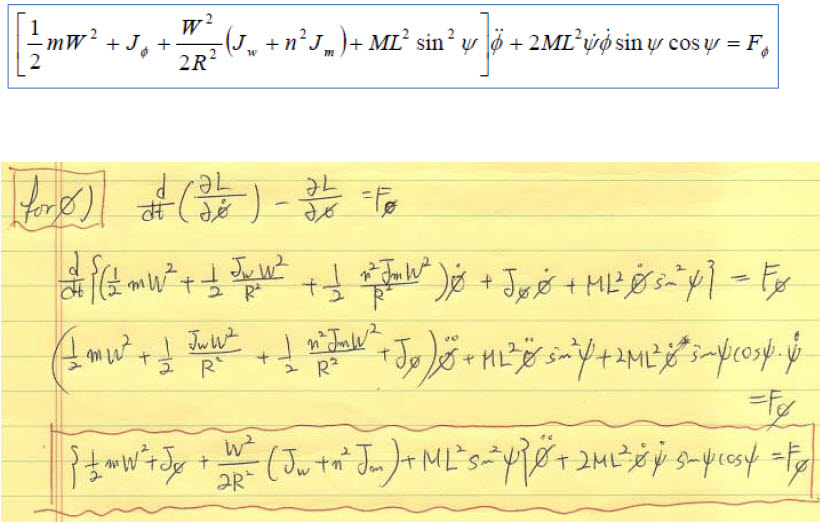
그리고, phi 상태에 대한 라그랑지 방정식도 일치하고 있습니다.

그런데, psi 상태에 대한 라그랑지 방정식이 일치하질 않습니다. 어디서 정확히 차이가 나는가하면
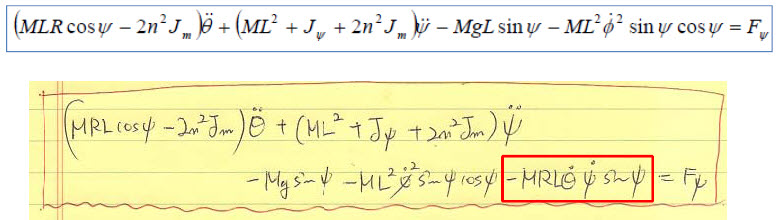
위에 표시된 항(-MRL dot_theta dot_psi sin(psi) )가 저는 있고, Yorihisa Yamamoto라는 분의 결과식에는 없습니다. 헉....ㅠㅠ 저 항은 이전의 MRL dot_theta cos (psi) 라는 항이 미분되면서 나타나는 두 항중 하나인데요. 그게 이상하죠. 미분된 두 항중 하나는 확인이 되었으니 말입니다.ㅠㅠ. 어디선가 고수한 홀연히 나타나서, PinkWink님 여기를 잘못 유도하셨군요.. 라고 속 시원히 말씀해주시면 좋겠는데 말이죠...ㅠㅠ (갑자기 저의 지도교수님 말씀이 생각납니다. - 넌 머리가 왜 이리 나쁘냐...ㅠㅠ) 잉~~~!!
그럼 혹시 정말 0.001%의 확률로 제가 맞다고 치죠..^^ 그럼 왜 Yorihisa Yamamoto라는 분의 문서에서 저 항이 없는데도 레고의 마인드스톰을 잘 제어가 되는가?? 라는 의문을 가지게 될 수도 있습니다만, 사실 레고사의 기술문서에서는 선형제어기를 사용하고 있습니다. 즉, 저한테는 있고, 기술문서에는 없는 저 항은, 동역학 모델을 선형화하다보면, 없어져 버립니다. 선형화 과정에서 어차피 없어질 항이기 때문에 큰 상관은 없습니다만...ㅠㅠ
하여간 또 새롭게 밝혀지기 전까지는 뭐 전 제가 맞다고 생각하고 진행해야죠^^...
이번에는 지난번에 이어서... 라그랑지 방정식을 유도하는 과정까지 진행했습니다.
'The Robot > Robot by PinkWink' 카테고리의 다른 글
| [밸런싱 로봇 만들기] 9. 기구부 재구성 및 모터 파라미터 수립 (56) | 2010/06/30 |
|---|---|
| [밸런싱 로봇 만들기] 8. 동역학 모델 구축하기 (최종) (24) | 2010/06/22 |
| [밸런싱 로봇 만들기] 7. Lego Mindstorm 동역학 따라하기 (32) | 2010/06/20 |
| [밸런싱 로봇 만들기] 6. Yaw 움직임을 포함한 동역학 (2) (16) | 2010/06/14 |
| [밸런싱 로봇 만들기] 5. Yaw 움직임을 포함한 동역학 (1) (16) | 2010/06/12 |
| [밸런싱 로봇 만들기] 4. 기구적인 파라미터 찾기 (32) | 2010/06/01 |
| [밸런싱 로봇 만들기] 3. 동역학 모델 구성하기 (40) | 2010/05/18 |
| [밸런싱 로봇 만들기] 2. 로봇 기구부 구성하기... (28) | 2010/05/12 |


처음 댓글을 남기게 되네요 ^^;
음.. 좋은내용입니다만... 무슨소리인지 모르게써요 ㅠ.ㅠ
그리고 광고가 중간중간있어서.. 어라 내용이 이거 뿐인가 하는 착각이 자꾸만 드네요
뭔소리인지도 모르겠고. 광고가 너무많아 보기도불편한데도 불구하고. 좋은 내용(?)이라고 해주셨군요.
수식을 자세히 보려니 머리가 아파서요 ㅋㅋ
저도 로봇에 관심은 많지만 이넘의 수학이 자꾸만 발목을 잡네요 ^^;
그 수학은 사람가리지 않고 발목을 잡습니다.
제 발목도 잡힌지 오랩니다.^^
노랑색 노트를 보니 아인슈타인이 연상된다는,,, 사인받아놔야 하는거 아닌가요
음... 머리크기는 비슷할지도 몰라요.. 푸하하하하
핑크윙크님을 보면서 도대체 저는 무얼했나 싶습니다. ㅠ_ㅠ
혹시 전공이 메카(기계)쪽의 제어전공이십니까?
저는 전자공학과 제어전공인데 라그랑지 동역학만 보면 머리가 다 아프네여 ㅠㅠ
저는.. 그냥 제어전공입니다.^^
제어계측공학과출신이거든요....^^
안녕하세요.. PinkWink님 블로그와 레고 NXT 배포 문서를 통해서 Segway를 만들고 있는데요.. 동역학 해석하는 부분이 -- 머리가 아프네요 ㅎ
동작은 하지만 제대로 알지 못하기 때문에 세부적으로 공부중입니다만,
동역학을 하지 않아서 궁금한점 질문 드릴께요..ㅡㅜ
전개에서 보면 x_m = R*theta*cosine phi 인데요 x_l 시간미분전개를 보면 x_m은 phi 항목을 미분하지 않았는데, 두 번째 항 W/2sin(phi)를 할때는 phi를 시간항에 대해서 미분합니다. 둘의 차이점을 알 수 있을까요? dx_l/dt 에서 R(dtheta/dt)cos(phi)+ (W/2)sin(phi)*(dphi/dt) 여기서 앞의 항과 두 번째 항에서 phi 미분을 하고 안하고의 차이가 있나요? -0-
네.. 항상 그 부분이 좀 슬프지요...^^
좌표 (xm, ym, zm)의 속도는 phi의 영향을 받지 않기 때문입니다.
그것은 phi가 (xm,ym,zm)을 중심으로 한 회전각도이기 때문이구요.
잘 보고 있습니다. 그런데 제가 수식을 살펴보다가 궁금해서 댓글을 다는데요..~
맨 처음 수식에서 왼쪽과 오른쪽 바퀴의 x,y 의 미분값을 구하셨는데 Rθsinφ*dφ 이 텀이 빠진것 아닌가요? 올려주신데로 계산하면 수식이 간단해서져 금방 풀수 있는데 미분시 생략된거 같아서요~
계산하다가 이것때문에 진행이 안되고 있습니다 ㅠㅠㅠ
phi에 대한 미분을 수행하지 않은 이유는
두 바퀴의 중심에 대한 변화율에 phi가 관여를 하지 않기 때문입니다.
http://www.pinkwink.kr/326
의 초반부에 언급을 했습니다.
앗~ ㅋ 감사합니다~ 이제 이해가 되네요~ ㅠㅠ
다시 열심히 풀어보겠습니다~ ㅋㅋ
네 다행입니다. 좋은 성과 있으시길 바랍니다.^^
비밀댓글입니다
흠.. 동역학 책 어디든 Lagrangian Method에 대해 다루는 책이 있다면 괜찮을겁니다. 라그랑지 방법은 공식화 되어 있어서 한 번 익혀 두면 쉽게 적용이 가능해집니다.