검색결과 리스트
글
라플라스 변환은 어떤한 함수 f(t)에서 다른 함수로의 변환으로, 선형동역하계와 같은 미분방정식을 풀 때 유용하게 사용된다. 피에르시몽 라플라스의 이름을 따 붙였다. (출처 : 위키피아) 본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보조 자료 이외의 목적이 없음을 알립니다. |
라플라스 변환

위에 라플라스변환의 정의가 나타나 있습니다.

라플라스변환의 정의를 이용해서 "1"을 라플라스변환한 결과입니다. 그러나, 위 정의식을 계속 사용한다는 것은 뭐 힘든일이겠지요^?^. 그래서

저와 같이 변환표를 이용합니다.
라플라스 역변환

위는 라플라스 역변환표입니다. 뭐 당연히 라플라스 변환표의 반대겠지요^^. 라플라스 역변환의 정의는 아주 복잡해서 손으로 푸는 것은 어렵습니다. 그래서 위 역변환표에 가장 가까운 형태로 식의 형태로 바꾸어가는 겁니다.

위의 예제를 보면 무슨 말인지 알 수 있을겁니다.

위 예제는 항별나누기를 이용해서 식을 분리하고, 라플라스 변환이 가지는 선형성을 이용해서 각각을 역변환하는 것입니다.

위 예제는 흔히 말하는 유수정리(Residue Theorem)의 부분분수 전개를 이용한 것입니다. 보통은 위 전개방식은 분모를 영으로 만드는 것을 대입한다고 외웁니다.^^.

이 라플라스 변환과 역변환은 미방의 풀이에 큰 장점을 가지게 되는데요 일단 도함수를 변환하면 위 정리와 같습니다.

미방을 라플라스 변환하고 대수방정식화된 식의 해를 찾고 다시 역변환하는 과정을 거치게 됩니다.

위 간단한 예를 보면

위와 같이 초기값을 고려하여 라플라스변환하고 라플라스변환된 식을 푼다음 다시 역변환으로 그 해를 찾는 것입니다.
Translation Theorem

시간영역에서 지수함수는 라플라스 변환을 하고 나면 단순 평행이동이 되어있습니다.

이를 이용하면 위 예제들 역시 간단히 그 해를 찾을 수 있습니다.
Derivatives of Transforms

시간영역에서 시간의 급수형태의 함수를 라플라스변환하면 라플라스 도메인 영역에 대한 미분형태로 나타나게 됩니다.
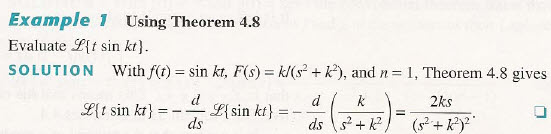
'The Robot > Theory' 카테고리의 다른 글
| [공학입문설계] 팀워크와 팀워크 기술 (14) | 2009/09/16 |
|---|---|
| [공업수학] 행렬식 determinant (4) | 2009/09/14 |
| [공업수학] 행렬의 기초 (12) | 2009/09/07 |
| [선형변환] 라플라스 변환 (Laplace Transform) (14) | 2009/09/04 |
| [C/C++] 선택문 (조건문) (6) | 2009/09/02 |
| [공학입문설계] 문제의 정의 및 공학설계 단계 (6) | 2009/09/02 |
| [공업수학] 벡터공간 (6) | 2009/08/30 |
| [공업수학] 벡터를 이용한 직선과 평면의 표현 (4) | 2009/08/30 |
설정
트랙백
-
Laplace Transform.
Trackback from Devjin`s Blog!
2010/04/24 14:12
[ DELETE ]
발등에 불이 떨어졌습니다...ㅜ 혹시 이문제를 풀어 보실분 계신가요? 마지막 9번 문제의 초기값은 x(0) = 1, y(0) =0 입니다. 학기중에 바쁜단 핑계로 블로그 시작을 안하고있었는데.. 이런글로 첫글을 쓰게되에 아쉽게 되었네요. 누구탓을 하겠습니까. 수업시간에 열심히 졸았던 저가 후회스럽네요..ㅠㅠ
 Laplace Transform -1.pdf
Laplace Transform -1.pdf

이 자식,, 라플라스 변환...날 괴롭히던걸 생각하면 후후 ㅡ.ㅡ;;
라플라스는 지금 저도 괴롭히네요..
딱 쓸만큼은 알고있는데...이거 수업을 해야하니...^^
이거슨 먹는것임?ㅎㅎㅎㅎㅎㅎ
머리로 먹어버려야 하는 건가봅니다..ㅋㅋ
부탁이 하나 있는데요..
혹시 시간있으시면.. 제 라플라스변환 문제좀 풀어주시면 안될까요..
9문제인데 전 완전 모르겠어서 이게 어려운건지 쉬운건지도 몰라서..
정말 부탁드립니다..;; 조금만이라도..흑흑
수고하세요 ㅎ
어려울것 같습니다.. ㅜㅜ
대부분의 블로그들이 질문과답변 게시판이 없는 이유는 자신의 포스팅내에서 공유와 간단한 질문에 답변을 유지하고 토론하는 것이기 때문인가요??^^
일단 어렵다고 하신 문제를 포스팅해보시면, 제가 보긴 하겠습니다 (저한테 트랙백을 보내세요. 관련글에... )
그러나 단 한 문제도 못풀어드릴수도 있습니다...^^
글올렸습니다.. 트랙백이 이게 맞는건지 잘몰라서요..ㅎ
어쨋든 관심가져주셔서 감사합니다.
어떻게든 열심히 풀도록 노력해봐야죠.
아 그리고 핑크윙크님이 올려주신글이 많이 도움이 되네요.
정말 여기는 저에겐 보물단지 같은 곳 입니다.ㅎㅎ
네... 좋은 답변을 구하실 수 있으셔야할 텐데 말이죠.
저도 보겠습니다.^^
쥔장님 좋은 글 많이 읽던도중 궁금한게 생겼는데 질문좀 하겠습니다..^^;;
그 라플라스 역변환에서 부분분수 나누는 부분에서요, 분모를 0으로 만는것 같은 모양인데요, 만약 중근이 분모에 있다면 어떻게 되는지 궁금합니다~
실제 유수정리에서 사용할 수도 있지만,
그와 같은 경우는
A s + B
-------------
(s + a )^2
이렇게 두고 전개해서 항등식의 풀이를 가지는 것도 괜찮습니다.^^
한개만 더요..^^;;;;;
부분 분수 나누는 부분에 관한거 한개 더 인데여,,,
만약 분모에 허수근을 갖는 형태 그러니까 (s^2 + 1) 이런형태가 껴있으면
어떻게 해야 하나요,,??? 바쁘신데 궁금한게 많아서 죄송해요^^;;;
변환공식 중 그와 같은 경우를 가지는 것이 sin과 cos이 있습니다. 즉, 말씀하신 형태에서 더 진행하는 것이 아니라 그 상태에서 역변환을 시도하시면 됩니다.
우왕.. 감사해요 많이 알고 가여..^ㅡ^ (꾸벅)
네.. 도움이 되셨다니 저도 좋습니다...^^