검색결과 리스트
글
본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보조 자료 이외의 목적이 없음을 알립니다. |
행렬의 소개
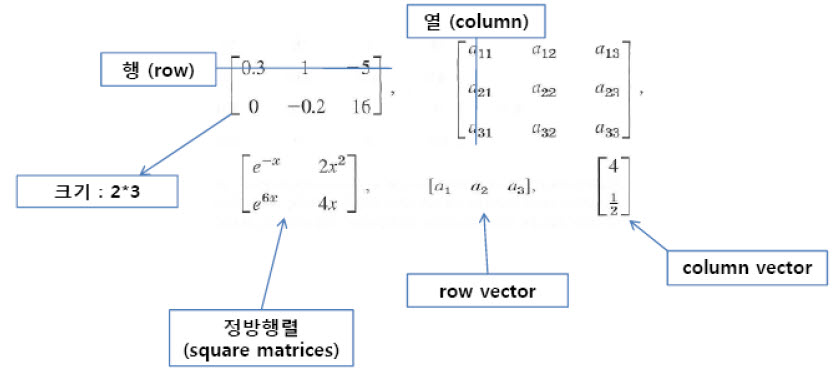
행렬은 숫자를 행(가로)과 열(세로)로 배열한 것입니다. 위 그림을 보면 (행의 개수)*(열의 개수)로 표기한 것을 행렬의 크기라고 하고, 행과 열의 개수가 같은 것을 정방행렬이라고 합니다. 행렬의 덧셈과 곱셈등은 참고자료를 보시고...

위에서 처럼 행과 열을 바꾼것을 전치(transpose) 행렬이라고 합니다.
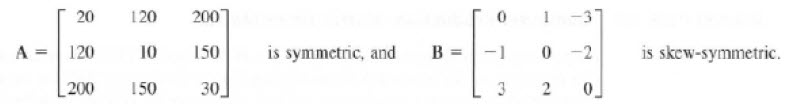
주 대각선상을 기준으로 대칭이 되는 행렬을 대칭(symmetric)행렬이라고 하고, 부호가 반대인것을 skew-symmetric이라고 합니다.
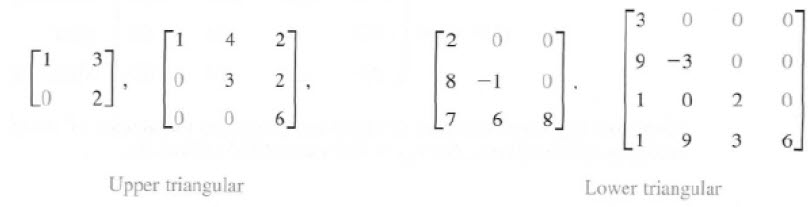
주 대각선상을 기준으로 그 아래가 다 0인 행렬을 upper triangular 행렬, 그 위가 다 0인 행렬을 lower triangular 행렬이라고 합니다.
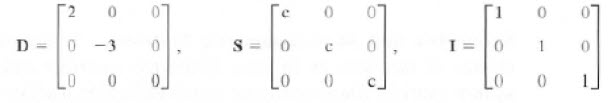
주 대각선상을 제외하고 모두 0인 행렬을 대각(diagonal)행렬이라고 하고 주 대각선상에 모두 1만 있는 행렬을 단위행렬이라고 합니다. 단위행렬의 상수배인 행렬을 스칼라 행렬이라고 합니다.
행 연산을 통한 연립방정식의 해법
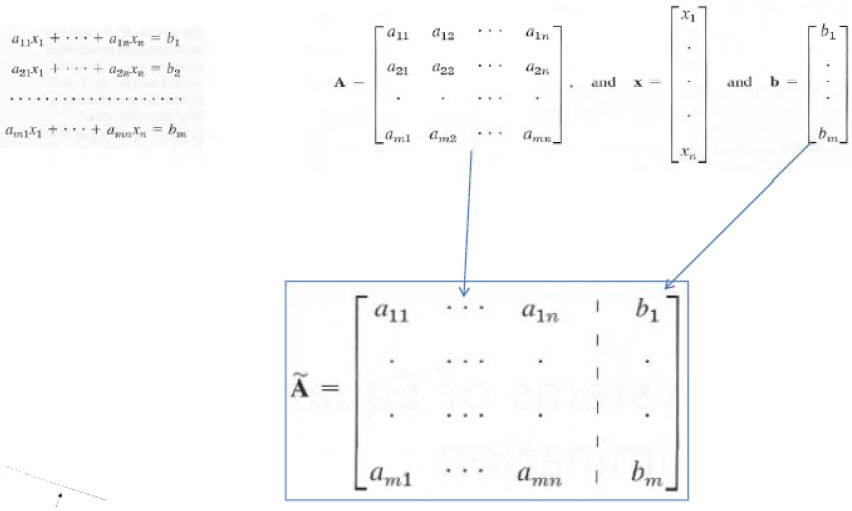
위 그림처럼 연립방정식의 계수를 모아둔 행렬을 계수행렬이라고 하고 그 계수행렬에 미지수 x의 계수가 아닌 bi들을 모아둔것을 열로 추가한 행렬을 확장행렬이라고 합니다.

위 규칙에 따라 확장행렬을 계산해 가면 연립방정식의 해를 구할 수 있습니다.
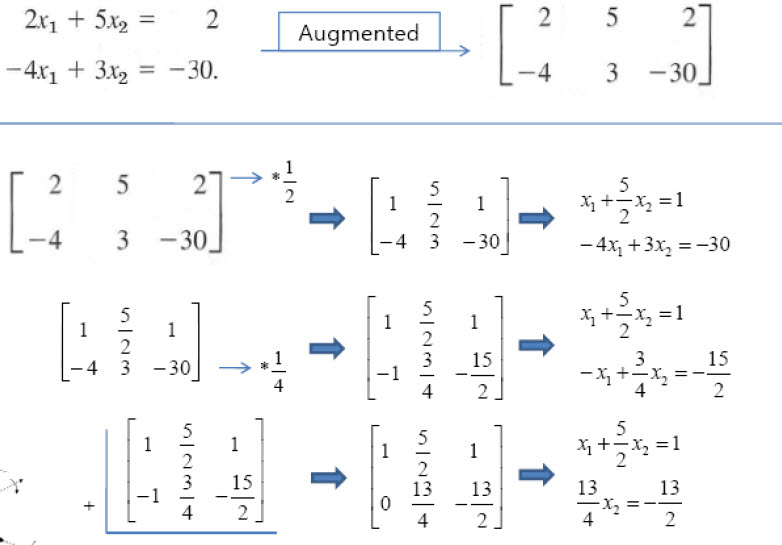
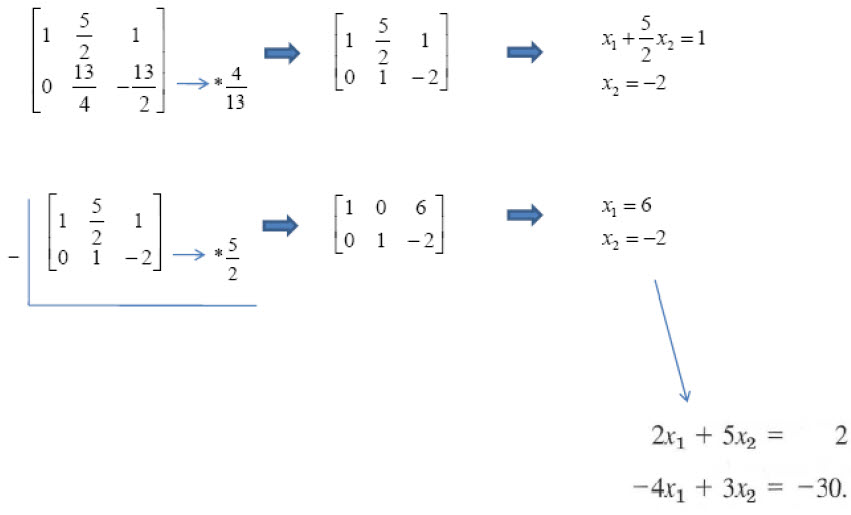
위의 예제는 간단하게 확장행렬의 행연산 과정과 실제 연립방정식을 푸는 과정을 같이 놓고 어떤 원리인지를 설명하고 있습니다.
Rank

선형독립인 행의 숫자를 Rank라고 합니다. 이 Rank가 Full이면 단 하나의 해가 존재할 수 있습니다.
'The Robot > Theory' 카테고리의 다른 글
| [공업수학] 역행렬 (Inverse Matrix) (16) | 2009/09/23 |
|---|---|
| [공학입문설계] 팀워크와 팀워크 기술 (14) | 2009/09/16 |
| [공업수학] 행렬식 determinant (4) | 2009/09/14 |
| [공업수학] 행렬의 기초 (12) | 2009/09/07 |
| [선형변환] 라플라스 변환 (Laplace Transform) (14) | 2009/09/04 |
| [C/C++] 선택문 (조건문) (6) | 2009/09/02 |
| [공학입문설계] 문제의 정의 및 공학설계 단계 (6) | 2009/09/02 |
| [공업수학] 벡터공간 (6) | 2009/08/30 |
 08 Matrix 01.pdf
08 Matrix 01.pdf

걍 패스...
이젠 기억도 안납니다. ㅎㅎㅎㅎㅎ
ㅎㅎ... 저도 패스~~~~
공업수학은 무엇? 먹는것인가?ㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎ
아작아작 씹어먹고 싶지만... ㅎㅎ^^
봐도모르겟다......
내일 시험인데 수학..
역행렬 행렬 ....허얽..
고2 실업계 수학 쫌 쉽게 설명해주실수없나요 ..
응?? 이건 공대 2학년을 대상으로 한 글인데요^^
고1인데 내일 학교에서 시험보는데 미국과정이랑 같아서 좋아요!!
도움 많이 됐습니다!!
네.. 도움이 되면 좋겠습니다.^^
공업수학 떠난지 5년이 지나서 다시 공부해볼까하고 들어 왔습니다. 이해가 빠르고 좋아요 감사합니다. 계속 여기로 와서 공부할게요 ^^
네.. 감사합니다. 저도 도움이 되었다니.. 기분이 좋군요...^%^
...고2에게는 너무 어려운...
이는 대학과정입니다.