검색결과 리스트
글
이번에는 지난번 선형동역학의 상태방정식 표현에 이어 대표적인 선형제어기인 LQR에 대해 이야기를 할려고합니다. 깊이있는 이야기가 아니라 그저 소개와 함께 실제로는 어떻게 LQR 제어 게인을 얻는지에 관한 이야기입니다.
|
|
|
| 기본적인 LQR의 개념 ! |
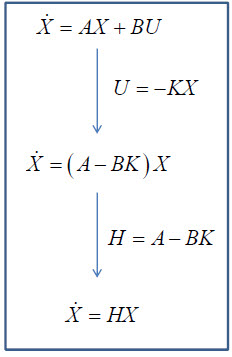
일반적인 선형시스템의 상태방정식은 dot_X = A*X+B*U의 형태입니다. 거기서 제어입력 U를
U=-KX
로 두고 다시 정리하면
dot_X=(A-B*K)*X
가 되는데요. 이걸 다시 H=A-BK로 두고 위와 같이 정리해둘 수 있습니다.

일단 성능지표(performance index)라고 하는 것을 위와 같이 생각해 볼 수 있습니다. 위의 상태 X는 벡터의 형태이기 때문에 사실상은 각 상태의 제곱의 합으로 표현한 것입니다. 상태의 제곱의 합이 작을 수록 좋은 것이지요. 결국 위의 정능지표를 최소화하는 뭔가가 필요한 것입니다.

이제 다시 일반적인 시스템에서 위의 수식을 만족하면 시스템은 안정(stable)하다고 볼 수 있습니다. 그러면, 그렇게 만들어주는 행렬 P를 찾으면 되는 것이지요.
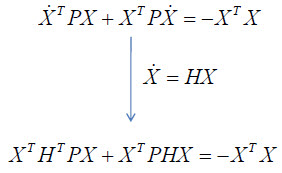
그것을 대입해서 정리하면 됩니다. 그러면 위의 마지막 수식에서
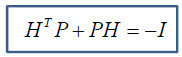
이걸 만족하는 P,H를 찾으면 되죠. 문제는 식하나에 미지수가 2개네요.

처음 생각했던 성능지표에 다시 대입해서 풀면

를 찾을 수 있습니다. 이제
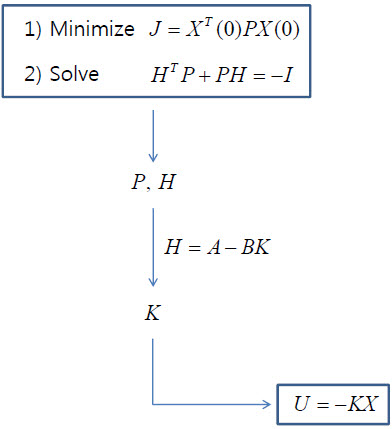
위의 1,2번 식을 만족하는 미지수 P,H를 찾으면, 제어게인 K를 찾을 수 있습니다.
그런데 일반적으로 성능지표는 각 상태에 가중치를 줄 수 있고, 제어입력의 크기에 대해서도 가중치를 설정할 수 있도록
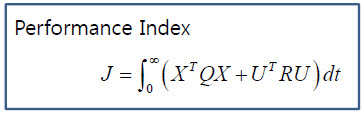
를 많이 사용하는 편입니다. 문제는 성능지표를 저렇게 두면, 손으로 푸는게 좀 어렵고 귀찮습니다. 그래서 많이 사용하는 것이 당연히 MATLAB이지요^^
| MATLAB을 이용한 LQR 게인 구하기 ! |
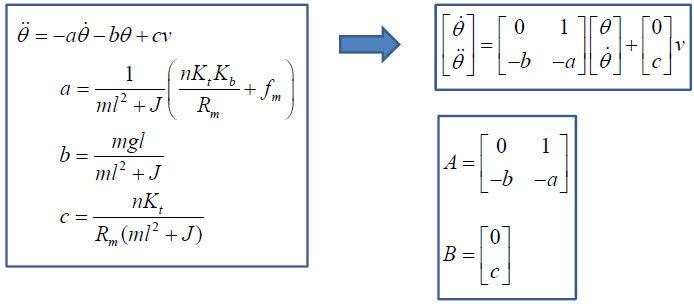
지난 시간까지 우리가 다루던 시스템의 상태방정식입니다. 여기서 A, B행렬을 얻을 수 있지요.

그리고, Q, R을 적절히 선정하고 MATLAB에서 LQR이라는 명령을 사용해주면 끝납니다.^^ 쉽죠^^
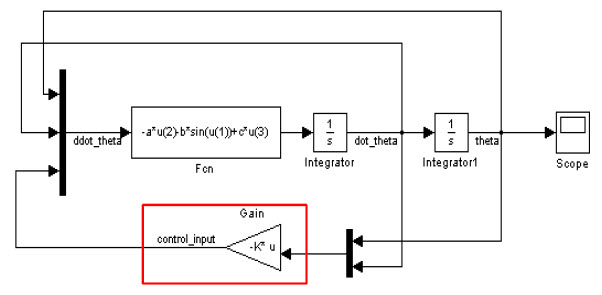
위 그림은 시뮬링크에서 LQR게인을 적용한 부분입니다.
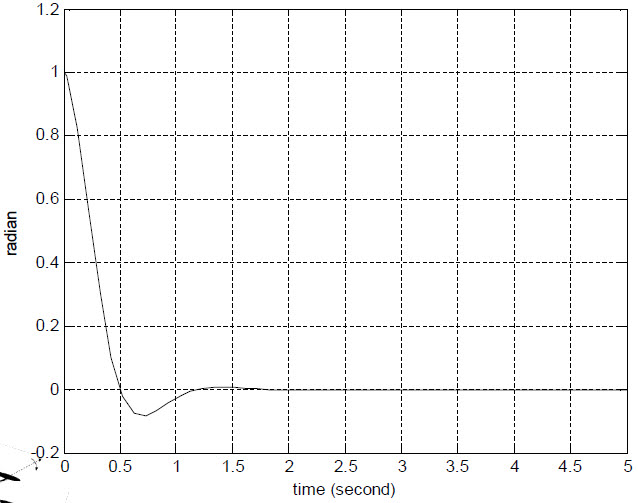
이것은 그 결과이지요. 자유운동을 시켰을 때 보다 확실히 성능이 좋아졌네요. 이렇게 되면, 아마 Q, R값을 조절해 보면 좀더 성능이 좋아 질 것입니다.^^
'The Robot > ControlTheory' 카테고리의 다른 글
| 델타형 병렬 로봇의 역기구학을 단순 기하학적으로 손쉽게 해석해보기 (8) | 2014/04/25 |
|---|---|
| 회전형 역진자 시스템의 동역학 Rotary Inverted Pendulum (8) | 2010/12/27 |
| [시스템 시뮬레이션 연재] 6. 경로추적 (tracking) (26) | 2010/08/16 |
| [시스템 시뮬레이션 연재] 5. LQR 제어기 설계 (26) | 2010/08/13 |
| [시스템 시뮬레이션 연재] 4. 시스템의 선형화 (2) | 2010/08/12 |
| [시스템 시뮬레이션 연재] 3. 동역학 MATLAB으로 시뮬레이션 하기 (18) | 2010/08/11 |
| [시스템 시뮬레이션 연재] 2. 구동원으로 DC 모터 고려하기 (56) | 2010/08/11 |
| [시스템 시뮬레이션 연재] 1. 라그랑지 방법을 이용한 동역학 모델 구축하기 (20) | 2010/08/09 |


오늘은 날이 좀 풀린듯 합니다.
전 사실 에어컨으로 인해 온도의 변화를 잘 못느낀답니다.. 클클^^
LQR 제어기 설계, 시스템 시뮬레이션 용어를 기억해 봅니다
히히. 죄송합니다.. 뭔가 평범한 글을 적어야하는건데 말이죠^^
저도...다른 분들이 궁금+경외하는 단어들로 이루어진 블로깅을 해보고 싶습니다만...^^;; 이렇게 댓글을 다는 걸로 만족. ㅋㅋㅋ
히히.. 사실 저희쪽 전공하신 분들이 보시면
그저 피식 웃을 수 밖에 없는 기초적인 거랍니다.
그저... 이런거라도 포스팅하는... 포스팅소재 고갈이 힘듭니다..ㅠㅠ
"일반적인 시스템에서 위의 수식을 만족하면 시스템은 안정(stable)" 이 부분이 이해가 안되네요 ㅜㅜ d/dt(X^TPX)=-X^TX 여기서 P가 무슨 의미로 들어가 있는거죠? 혹시 제가 놓친게 있나요?
일반적으로 시간의 함수 x가 있다면, dot(x) = x 라면, 대표적으로 지수함수인 x=e^t 를 예로 들 수 있습니다. 시간이 흘러갈 수록 (즉, t가 커질수록) 함수값은 발산하게 됩니다. 그러나 dot(x) = -x를 만족하단다면, 예를 들면, x=e^(-t) 이라면, 시간이 흐를 수록 x는 '0'으로 수렴하여 안정화됩니다. 여기서는 단순한 상태가 아니라 상태들의 모임인 벡터의 개념이고, 또 본래 시스템이 안정한지 아닌진 모르겠지만, dot(X^T * X) = -x^T * x가 되게끔 해주는 어떤 행렬이 있다면, 혹은 존재할 수 있어서, dot(X^T * P * X) = -x^T * x 이 되면 안정화될 것입니다.
그럼 그냥 X^T * X이 dot(X^T * X)와 부호가 반대고 절대값이 '비례한다면' 시스템이 안정화 될 수 있는건데 그 비례상수는 벡터의 구성요소인 상태변수별로 달라질 수 있기 때문에 각 상태변수마다 다른 값을 곱해줄 수 있는 대각행렬을 구해야 한다고 생각하면 될까요??
틀린 설명이 아닙니다만, 사실 오히려 제가 설명이 부족했나봅니다. Dorf의 현대제어시스템이나, 최적제어에 관련된 책을 찾아보시면, 좀더 명쾌이 이해하실 수 있지 않을까합니다. 설명능력의 부족을 사과드립니다.ㅠㅠ 아 그리고, 위의 행렬 P는 대칭행렬입니다.
아니에요;;; PinkWink님 블로그에서 많은 것들을 배워가고 있어 항상 감사하게 생각하고 있습니다;; 알려주신 책들을 한번 찾아보겠습니다 ㅎㅎ 감사합니다
네.. 좋은 성과있으시길 바랍니다.^^
pinkwink님... 질문이 있는데요....쫌 쌩뚱맞을 수 있긴 하지만..
상태방정식이란 무엇이라고 생각하세요?? 단순히 LQR제어게인을 구하기 위해 존재하는 것이 아니라...
시스템에서 어떤 한 순간(lim t -> 0)에서의 상태가 어떠한지..그것을 표현해주는 것인가요??
상태방정식은 상태행렬로 표현된 식을 의미합니다. 상태행렬을 이용하면 시스템이 제어가능한지 관측가능한지 알 수 있고, 고유치를 조사해서 불안정한지 안정한지 알 수 있습니다. 물론 상태방정식과 전달함수간에 서로 변환도 가능합니다.
아하!!!!그렇군요....감사합니다.
상태방정식과 전달함수간 서로 변환이 가능하다라는 말씀이.. 이 둘이 하나의 시스템을 표현해 주는 방법들 중에 하나라는 말씀이신거죠??
그냥 표현일 뿐입니다. 이렇게 표현하나 저렇게 표현하나 원 시스템은 바뀌지 않을테니까요
궁금해요!
LQR제어에 대해서 아무것도 모르고( 첨 들어봤어요 ㅋ) 위에서 설명하신 부분을 따라해 보고 있는데요..
이득을 얻기 위해서 a,b,c 부분의 값을 넣어줘야 한다라고 생각되는데
이 부분에 대해서 설명좀 해주세요..ㅡㅜ
이 글의 a,b,c값은 연재의 이전 글에서 구해놓은 값입니다.
연재 목차는 글 상단에 있답니다.
질문있습니다.
내용의 중간에 상태의 제곱의 합이 작을수록 좋다고 하셨는데 아직 내용파악이 부족해서 그런건지 잘 이해가 안되네요;;
모든 상태가 '0'로 가기를 바라고 있습니다.
그 중에서 일종의 RMS처럼.. 제곱의 합을 최소화하도록 한겁니다.
그럼.. 각 상태의 크기를 '0'으로 할 수 있을 테니까요.
좋은자료 감사합니다!
혹시 MPC나 DOB도 자주사용하시나요? 최근에 외란관측기(DOB)에 관해서 공부중인데 간단한 알고리즘인데도 불구하고 실제로적용해서 시뮬레이션 하는건 만만치가않네요... ㅎㅎ
저는 아주 예전에 시뮬레이션만 좀 했던 기억이 나네요.
그러나 뭐 모든일이 그렇듯.. 지금은 잘 생각이.. ㅠㅠ
이런.. 도움이 되어드리지 못했네요...ㅠㅠ
아주 초보자입니다 ㅠ
LQR 매틀랩
에서 K=lqr(A,B,Q,QR)
여기서 에이랑비는 상태공간구하면얻어지는걸로 알고잇는데
케이랑 큐랑 큐알 이 의미하는것이 무었인지 알고싶어요 (개념)
Q와 R은 사용자가 설정하는 것입니다.
Q는 각 상태별로 중요도를 설정하는 가중치이고
R은 출력에 대한 가중치입니다.
감사합니다.
본문내용에서 Q R을 적절히 조절하면 성능변화를 볼 수 있다고 하셔는데 이 부분을 구체적으로
각 값 Q R 이 커지거나 작아지면 어떻게 성능이 변화되는지 알 수 있을까요?
Q는 각 상태에 곱해집니다. 해당 상태만 특별히 더 중요하다면 그 요소만 다른 요소에 비해 좀 큰 값을 주면 됩니다.
R은 전체 제어입력을 다루는 것으로 값이 작아질 수로 전체 제어 입력이 좀 커집니다.