검색결과 리스트
글
이중적분
이번에는 2중적분에서 구간의 설정과 간단한 예제. 그리고 질량중심과 관성모멘트의 도출을 간단히 다뤄보겠습니다.
본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보조 자료 이외의 목적이 없음을 알립니다.
이번에는 2중적분에서 구간의 설정과 간단한 예제. 그리고 질량중심과 관성모멘트의 도출을 간단히 다뤄보겠습니다.
본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보조 자료 이외의 목적이 없음을 알립니다.
이중적분
이중적분을 위에서 처럼 순서로 생각해보면 두가지로 생각해 볼 수 있을 겁니다. (뭘 먼저 적분하는가.. 하는 문제 말이죠) 정적분이라고 생각해야하는 것이니 먼저 적분되는 쪽은 다른쪽 변수로 함수화된 구간으로 주어져야할 것입니다.
위 문제를 보죠.
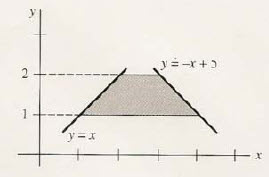
위 구간에서 이중적분을 수행해달라는 건데요.
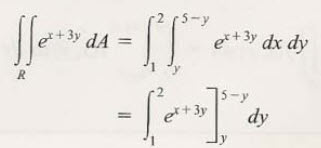
x쪽을 먼저 적분해야하는 걸로 보면, x=y부터 x=5-y까지적분한다고 생각할 수 있습니다.
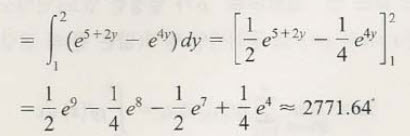
그러면 위와 같은 결과를 얻을 수 있지요.
그러나 위 문제를 보겠습니다.
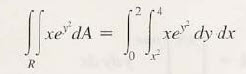
먼저 위와 같이 적분을
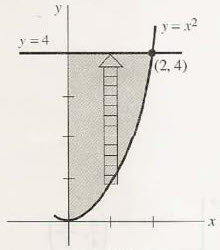
위 그림처럼 시도하게 되면, 문제가 하나 생깁니다. y제곱을 가진 지수함수를 적분하지 못하는 거죠. 그리니 반대 방향으로 생각합니다.
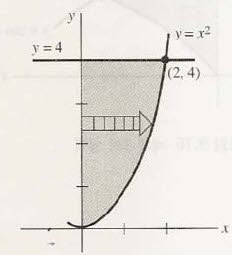
위 그림처럼 시도하면
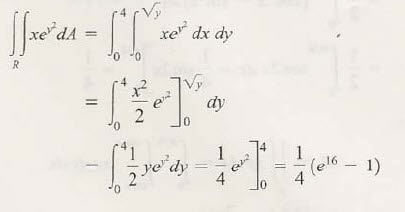
적분이 가능해 지는 거죠. 물론 적분구간에 대해서 조심하셔야합니다.
질량중심
밀도가 주어진 질량은 이중적분으로 도출할 수 있습니다.
밀도 함수도 주어졌으니 이중적분으로 일단 질량을 구하도록하죠
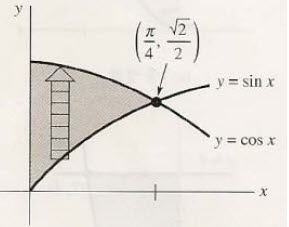
위 그림에 대해 생각하면
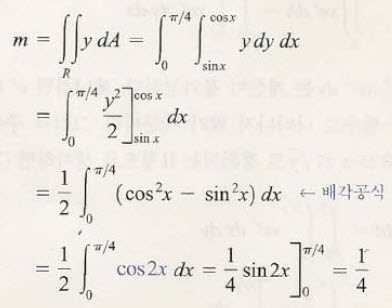
질량을 구할 수 있겠죠. 고등학교때 배운 삼각함수라는게 또 이렇게 사용된다는 것을 보면 고등학교때 좀 열심히 삼각함수할껄 하고 생각하는 학생들도 있을 겁니다.^^.
여기에 그 질량중심의 좌표를 구하는 과정입니다.
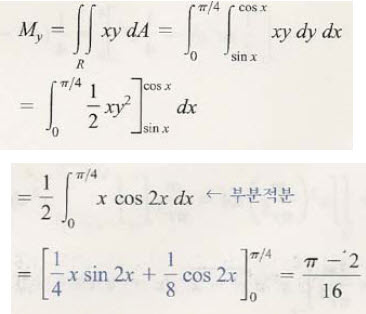
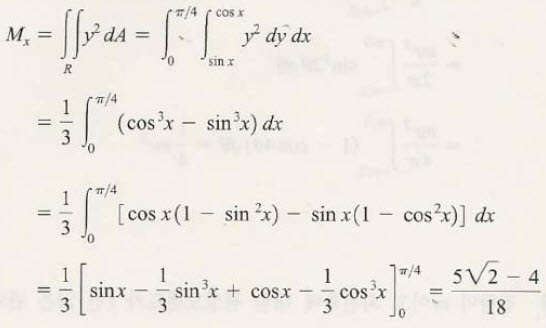
관성모멘트
관성모멘트의 도출 식인데요.
위 예제에 적용만 시켜보도록하면,
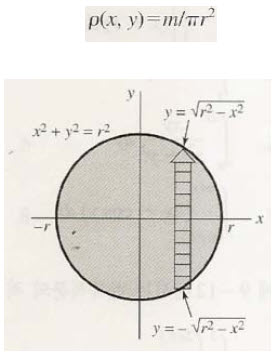
균일한 밀도라고 했고, 원판이니까 밀도함수의 위와같이 잡구요. 계사하면
되죠...^^
09 Vector 08.pdf'The Robot > Theory' 카테고리의 다른 글
| [공업수학] 면적분 (6) | 2009/11/26 |
|---|---|
| [공업수학] Green 정리 (2) | 2009/11/22 |
| [공업수학] 극좌표계에서의 이중적분 (4) | 2009/11/22 |
| [공업수학] 이중적분 (20) | 2009/11/15 |
| [공업수학] 경로의 무관성 (0) | 2009/11/15 |
| [C/C++] 재귀호출 (12) | 2009/11/15 |
| [공업수학] 선적분 curve integral (6) | 2009/11/10 |
| [공업수학] 벡터의 회전(curl)과 발산(divergence) (4) | 2009/11/10 |
설정
트랙백
http://pinkwink.kr/trackback/219
비밀댓글입니다
우와... 정말 감사합니다...
이런 행운이~~~~^^
머리가 비상하실거같다는 생각뿐 ㅋ
저런 머리가 비상했으면 벌써 졸업했어야죠...
전 좀 아둔하고 느려요... 그게 가끔 절 슬프게 한답니다...ㅜ.ㅜ
적분도 모르는데, 이중적분을.... 미오
히히.. 제 글이 몹시 이상하다는걸 잘 아시면서...^^
저기 죄송한데 맨밑에 그림에서 삼각함수공식이라는 부분이 뭔말인지 잘모르겠는데
설명좀 부탁드려요 님 ㅠ_ㅠ
네..^^. 말씀하신 부분은
x = r*sin(theta)
로 치환하라는 말입니다.
감사합니다 즐겁게보고갑니다 ^^
감사합니다. 즐거우셨다니 다행입니다.^^
음 담아가고싶은데 퍼가는 기능은 없나요 ㅜㅜ
퍼가기라는 기능은 없습니다.
http://stringsitsc.tistory.com/290
라는 글이 좋은 내용을 담고있답니다...^^
안녕하세요. 구글링하다가 들어왔어요. 이런 좋은데를 진작에 알았으면 좋았는데...
그나저나 이중적분 질문좀 할께요... 이해가 안되는게 있어서... 이중적분 2번째 문제에 대한 질문입니다. 적분 구간을 잡는 기준이 궁금해요.
두번째 문제 첫번째 풀이법에서 y구간을 x제곱~4 로 잡으셨는데 0~x제곱으로 해도 될거 같고... 두번째 풀이법에서 x구간을 0~루트y 로 잡으셨는데 루트y~2 로 해도 될거 같아서요.
확률과정 공부하다가 적분 구간때문에 구글링하다가 들어왔어요.PDF를 적분해야 되는데 이중적분 적분구간때문에 환장하겠음.. 제발 도움을
낮은 곳에서 높은 곳으로 수직선이라면 왼쪽에서 오른쪽으로 적분 구간을 잡는것과 같습니다. 다시 한번 이중적분이 시작되는 설명에서 보시면 방향을 설정해두었습니다.
관성모멘트 따라왔다가 @.@ㅋㅋㅋ 다른 글들도 끌리네요 ㅋㅋ
네... 좋은 공부되시고, 또 쉬엄쉬엄 하세요^^
비밀댓글입니다
네... 좋은 성과가 있으시길 바랍니다.^^
안녕하세요 이해가 안되서 질문 드리려고합니다 먼저 2차원에서 curve를 적분하면 면적이 되고 이중적분하면 부피가 되는데요 질량 중심에서 이중적분값은 질량이 나온다고했는데 단순 이중적분에서는 부피값이 나오는데 질량과 부피가 어떻게 같은 개념을 갖는지 궁금합니다
밀도의 이중적분이 질량이라는 이야기입니다.