검색결과 리스트
글
본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보조 자료 이외의 목적이 없음을 알립니다.
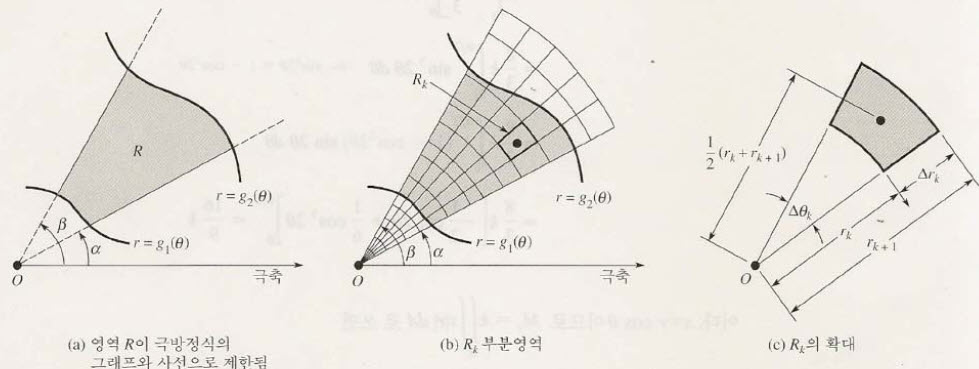
라고 생각할 수 있을 것입니다. 위 식에서 1/2(r_k+1 + r_k)의 부분은 반지름의 평균으로 볼 수 있겠네요. 그리고 delta r 과 delta theta 로 표현가능하구요.
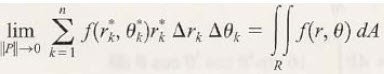
위 그림 (b)에서 무한등분으로 다시 표현하면 위 수식처럼 표현 가능합니다. 이중적분인것이죠.
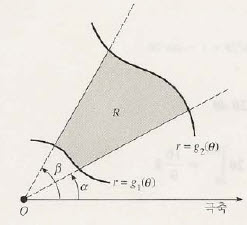
위 부채꼴에서의 이중적분을 다시 생각해보면
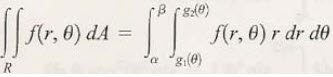
위와 같이 볼 수 있습니다. 극좌표계에서의 이중적분을 구성할 때는 r dr dtheta 를 생각해주면 되겠군요.
'The Robot > Theory' 카테고리의 다른 글
| [공업수학] Stokes 정리 (0) | 2009/12/02 |
|---|---|
| [공업수학] 면적분 (6) | 2009/11/26 |
| [공업수학] Green 정리 (2) | 2009/11/22 |
| [공업수학] 극좌표계에서의 이중적분 (4) | 2009/11/22 |
| [공업수학] 이중적분 (20) | 2009/11/15 |
| [공업수학] 경로의 무관성 (0) | 2009/11/15 |
| [C/C++] 재귀호출 (12) | 2009/11/15 |
| [공업수학] 선적분 curve integral (6) | 2009/11/10 |
 09 Vector 09.pdf
09 Vector 09.pdf

조만간 삼중적분 시간이 돌아오겠군요. ㅎㅎㅎ
역시 치매방지용으로 정석을 구매하시는 분 답게... 다음 순서를 알고계시는군요..ㅋㅋ^^ 아마 면적분 다음에 나올것같은데요^^
순서는 초등생도 알고 있을 것 같은데요. 이중적분다음에 삼중적분, 삼중적분 다음에 사중적분, 오중적분....ㅋㅋㅋ
ㅎㅎ 그런건가요?^^