검색결과 리스트
글
분명 여름인데... 비가오면서 그런건지 요즘 덥지가 않네요. 지금 시간이 밤 10시가 넘었는데, 제가 있는 건물 1층에는 내일 국제생물올림피아드대회 준비로 많은 사람들이 분주하게 움직이고 있네요.
오늘은 리액션휠에 대한 이야기를 할려고 합니다. 사실 이 부분은 참 창피한 이야기인데요. 아주 예전에 리액션휠에 대해 이야기를 했었습니다.[관련글] 그런데 이 때 제가 동역학을 잘 못 유도한 것을 알고 다시 수정본을 포스팅[관련글] 했는데요. 큭... 그것 마저 잘못되었더군요. 그래서 다시 합니다. 두 번째 포스팅 당시 sdfzz님의 질문에서 시작된 의문 덕분에 잘못된 것을 알았지요. 그 후 차일피일 미루다가 이렇게 다시 공부한 결과를 올려놓네요...
먼저 의문점의 시작을 이야기해야겠습니다.^^

이 책은 "The reaction wheel pendulum"이라는 책(이하 참조A)에서는
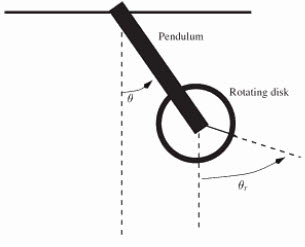
여기서

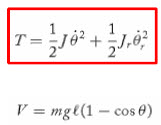
위의 운동에너지 부분이 마치 단순히 theta와 theta_r 즉, 막대기와 휠의 운둥에너지를 다룬듯이 보이고,
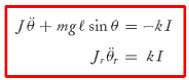
라그랑지안 방정식에서 모터의 토크가 두 상태에 다른 방향으로 인가된다고 설명하고 있습니다.
이제 또다른 참조

"Non-linear control for Underactuated Mechanical Systems"와

"Nonlinear control of the Reaction Wheel Pendulum"
위 두 참조 문헌(이하 참조B)에서는
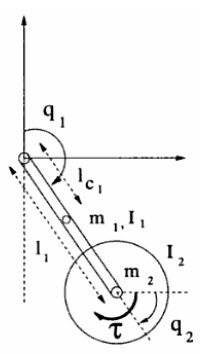
위에서

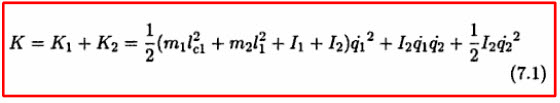
운동에너지를 고려할때, 참조A와 다른 모습을 보여주고 있는듯 보입니다.
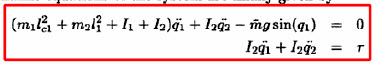
그리고, 마지막 단계, 라그랑지방정식에서 외력을 한쪽에만 모터토크가 들어가는 듯 모이는데요.
마치 다르게 유도된듯이 보이는 것이 당시 가졌던 의문입니다.
정리하면,
참조A는 운동에너지를 직선운동에너지와 회전운동에너지로 두고 있는데, 이때, 회전운동에너지는 단순히 두 물체(막대기와 휠)의 회전력만을 고려했고
참조B는 회전운동에너지를 고려할때, 참조A와는 달리 뭔가 하나 더 들어간듯이 보인다는 겁니다.
또한,
참조A는 라그랑지 방정식의 결과식에서 외력을 두 상태 모두에 인가를 했고,
참조B는 휠을 구동하는 모터 토크는 휠의 상태 q_2를 유도한 식에만 인가되어있다는
것으로 보이는 겁니다.
이제, 달라보이는 두 동역학유도과정을 비교해보겠습니다. 방법은 참조A를 변형하는 것인데요. 참조A의 치환된 문자들을 대입해보겠습니다.
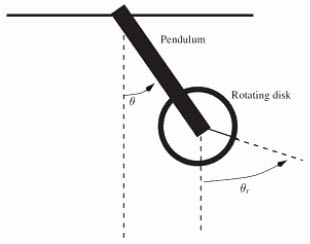
위 그림에서 참조A는 두 각 theta와 theta_r을 모두 절대좌표계의 각도로 보고있습니다.
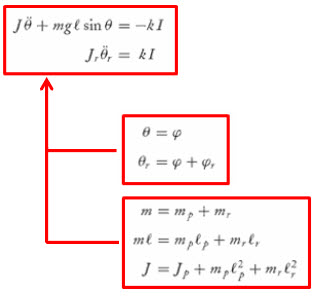
그래서, 참조A의 라그랑지 방정식 결과식에 위와같이 대입합니다. theta는 phi로 theta_r은 막대가 움직인 phi에 휠이 돌아간 phi_r을 더한 것으로, 나머지는 참조A가 본문에서 밝힌대로 본래의 치환을 돌려놓는 것입니다.
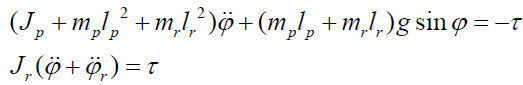
일차적으로 위와 같이 정리가 됩니다. 이를 참조B처럼 만들기 위해 모터 토크 tau를 다시 대입해서
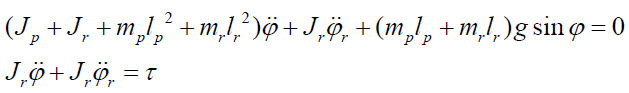
이렇게 만들어 볼 수 있습니다. 이 결과를 참조B와 비교하면
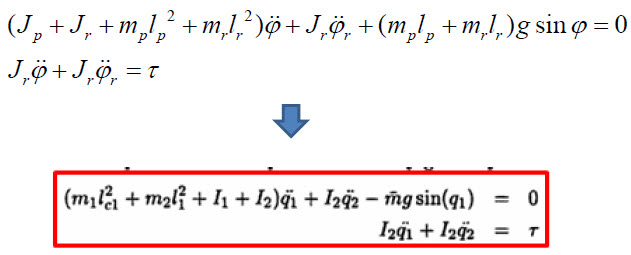
이렇습니다. 같네요. 즉, 참조A와 참조B의 동역학은 같은 식입니다. 여기서 위치에너지를 의미하는 부분 중력가속도 g가 있는 부분의 부호는 좌표원점을 어디로 보고, 초기상태를 어떻게 보았느냐의 차이라 달라도 다른게 아니라는...^^
즉, 단순히 눈으로보면 달라보이는 동역학이 사실 같은 동역학이라는 것이 중요합니다.
결국
참조A는 막대와 휠의 각도를 절대좌표에서 바라본것이고
참조B는 막대의 각도는 절대좌표에서 본 것이지만, 휠의 각도는 막대를 기준으로 본 상태좌표입니다.
결국 최초로 저에게 리액션휠의 동역학 분석을 질문하셨던, "정문님"님과 그 후 저에게 질문을 하셨던 "sdfzz"님 덕분에 제가 라그랑지 방법을 통한 동역학 유도에서 잘 못 알고 있던 부분, 혹은 고민하지 않았던 부분에 대한 고민을 하게 해 주신거라... 감사의 말씀을 전하고 싶습니다.^^.
하여간, 결론은
라그랑지 방법을 이용한 동역학 유도에서 각 상태를 절대좌표계에서 보는가 상대좌표계에서 보는가에 따라 조심스럽게 접근을 해야겠네요.
|
|
|
이제 다시, 저만의 것으로 만들기 위해 저도 따로 유도를 하겠습니다.
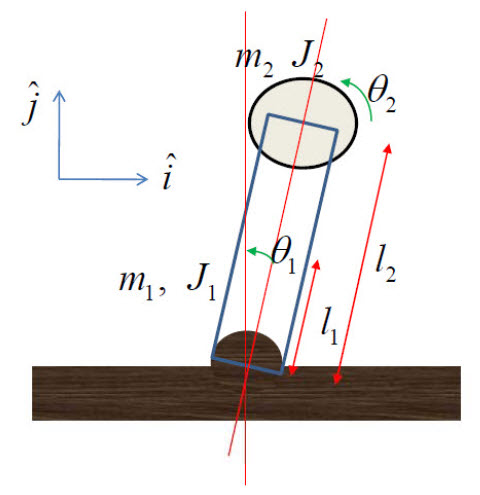
위 그림에서,
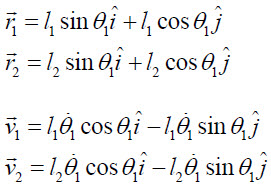
위치벡터와 그에 따른 속도벡터에서 운동에너지와 위치에너지는
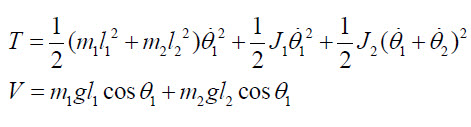
와 같습니다. 여기서 theta_2는 막대에서 본 상대각도입니다. 그러므로 운동에너지는 직선운동성분과 회전운동성분인데, 이 중 회전운동에너지는 theta_1에 대해서는 일반적인 상황과 같지만, 휠의 회전운동은 theta_1의 속도와 theta_2의 속도의 합에 대해 기술해야하는 것입니다.
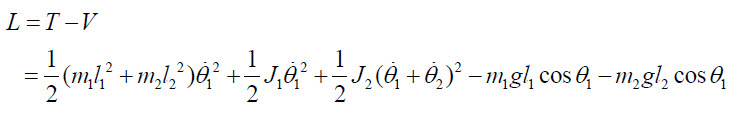
그럼 위의 라그랑지안이 나타나는데요
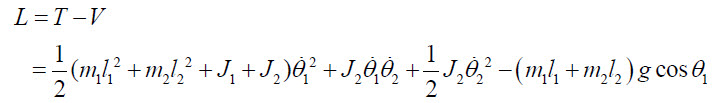
이 후 유도를 위해 좀 정리를 다시하고, theta_1에 대한 라그랑지 방정식은
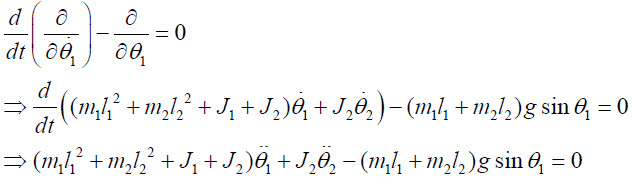
이렇습니다. 여기서 외력은 '0'입니다. (마찰 무시) theta_2에 대한 라그랑지 방정식은
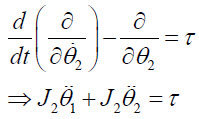
이렇습니다. 여기서는 모터의 토크가 외력으로 고려됩니다.
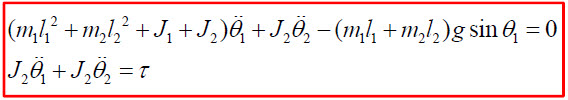
이렇게 해서, 리액션휠의 동역학의 라그랑지방정식을 얻었네요. 음... 이쯤이 결론이지 않을까하는데요^^
요즘 논문준비로 너무 바쁘게 보네는데, 큰일입니다. 밸런싱로봇 이야기도 해야하는데 말이죠.. ㅎㅎ
'The Robot > ControlTheory' 카테고리의 다른 글
| [시스템 시뮬레이션 연재] 3. 동역학 MATLAB으로 시뮬레이션 하기 (18) | 2010/08/11 |
|---|---|
| [시스템 시뮬레이션 연재] 2. 구동원으로 DC 모터 고려하기 (56) | 2010/08/11 |
| [시스템 시뮬레이션 연재] 1. 라그랑지 방법을 이용한 동역학 모델 구축하기 (20) | 2010/08/09 |
| Reaction Wheel Pendulum. 리액션 휠 펜들럼의 동역학 유도과정 (최종) (10) | 2010/07/14 |
| Reaction Wheel Pendulum. 리액션 휠 펜들럼의 동역학 유도과정 수정 (6) | 2010/06/15 |
| Reaction Wheel Pendulum. 리액션 휠 펜들럼의 동역학 및 시뮬레이션 (10) | 2010/05/14 |
| T-S 퍼지를 기본으로 한 선택적 선형화를 이용한 Two-Rotor (VTOL) 시스템 제어 (4) | 2010/04/19 |
| 밸런싱 로봇의 동역학 유도 (16) | 2010/01/03 |


어느새 최종인가요,, 잘모르는 불량한 학생으로 그동안 잘배웠어요,,ㅋㅋ
감사합니다.
크헉.. 슬픈 일입니다... 한 포스팅으로 처리할 수 있는걸 실수로 3개나 포스팅하다니...ㅠㅠ
-_-;; 저도 바빠서(믿거나 말거나) 한동안 못들어 와 봣는데 이렇게 정리해 주셔서 정말 감사합니다.
많이 배우고 가고요, 앞으로도 좋은 포스팅 부탁드립니다.
네.. 감사합니다.^^
저도 여기 와서 가끔 글을 읽었는데, 이렇게 댓글 쓰는건 처음이네요^^
잘 읽었습니다. 여기 블로그가 많은 도움이 되요~
네.. 감사합니다...^^
안녕하세요~ 질문이 있어서요 ㅎ
결론으로 나온 두 식에서 theta2에 대해서는 소거해버리고 theta1에 대한 식으로 나타낼 수 있다면,
두번째 식의 토크는 제어입력이 되는건가요?
그렇다고 한다면, 토크를 어떤식으로 제어해야 할까요?
보통 모터는 각속도를 측정하는거 같던데 말이죠..
해당식에서 토크는 제어입력입니다. 만약 DC모터라면 DC모터의 동역학적 방정식을 대입하면, 전압에 대해 나타납니다.
제가 아직 라그랑지에 대한 지식이 전혀 없어서 질문 드립니다.
결론으로 나온 두식이 차이가 먼가요??
두번째식은 토크에 관한 식인건 알겠는데, 첫번째 식은 멀 의미하는지 정확하게 모르겠네요 ㅠㅠ
어떤 수식을 유도과정없이 그 결과식을 놓고 의미를 말로 풀어서 설명을 완전히 할 수 없을 때가 더 많습니다.
이 경우도 마찬가지 입니다. 뭐 말을 만들어내면 할 수 있을진 모르지만, 그렇게 해본적은 없습니다.
라그랑지안 유도법대로 그 시작이 되는 식을 잘 적용하고 거기서 유도를 시작한것으로 결과식이 중요한것이 아니라 사실은 첫 부분과 그 개념이 중요합니다. 해당식도 마찬가지로 제가 실수했을 수도 있구요.