검색결과 리스트
글
본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보조 자료 이외의 목적이 없음을 알립니다. |
고유값과 고유벡터

위의 정의에서 보이지만, AK=(lambda)K 를 만족하는 lambda를 고유치, K를 고유벡터라고 합니다. 구하는 방법은 위 정의에서

위처럼 생각하면 됩니다. det(A-lambda I)=0를 풀면 됩니다.
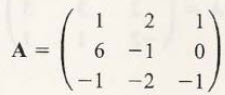
예를 들어 위의 A행렬의 고유치와 고유벡터를 구하는 과정을 보면

위 행렬식을 풀어서 lambda의 방정식이 나오는데 그걸 특성방정식이라고 합니다. 그 특성방정식을 풀면 근이 나오겠지요. 그 근을 고유치라고 합니다.

그리고 각 고유치를 다시 정의식에 대입하여 고유벡터를 구합니다. 그리고 보시다시피 고유벡터가 단하나 존재하는 것은 아닙니다.


만약 고유치가 복소값을 가진다면

위 정리처럼 복소고유치에 대해 복소 고유벡터를 가집니다.

그리고 삼각행렬이나 대각행렬은 그 고유값이 주대각원소들이 됩니다.
행렬의 거듭제곱 - Cayley-Hamilton 정리

제곱의 표현에서 행렬 A나 그 특성방정식은 같습니다.
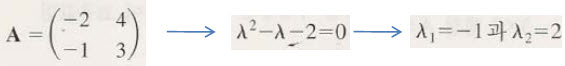
A행렬이 위와 같이 주어지고, 고유치를 구하기 위한 특성방정식을 찾고 고유치를 찾았습니다.
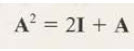
그 특성방정식과 같은 형태로 A행렬의 위 식을 만족합니다. 이것을 확장하면
위에서 처럼 계속 A의 거듭제곱을 표현할 수 있습니다.
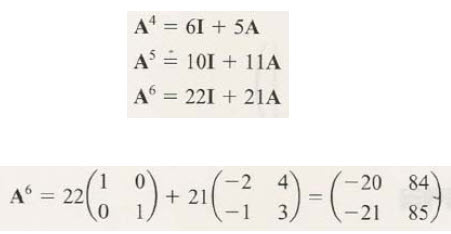
위의 거듭제곱을 좀 더 확장해서 생각해보면
A의 m승의 식이 위에서 처럼 I와 A로 표현된다면 그 계수는 그대로 고유치의 m승에 대해서도 적용될 수 있습니다.
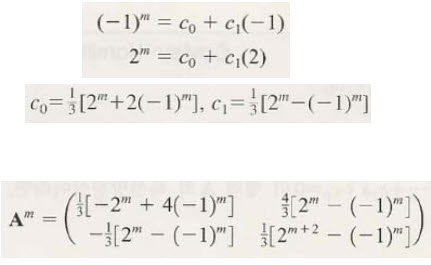
위에 그 과정이 나타나 있네요
직교행렬

대칭행렬의 정의입니다.



직교행렬이란 A의 전치행렬과 A의 역행렬이 같은 행렬을 직교행렬이라고 합니다.
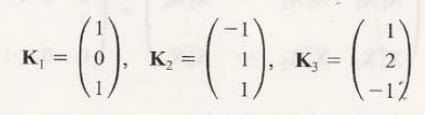
어떤 행렬의 고유벡터가 위와같이 나왔다면
각 고유벡터의 크기(norm)를 1로 만들기 위해 그 크기를 구해서 다시 나누고
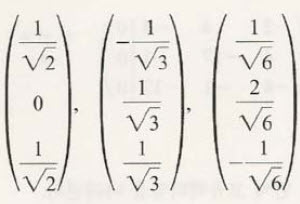
그것을 다시 행렬로 만들면
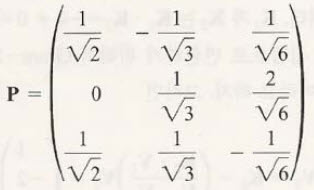
해당 고유벡터를 가지는 행렬의 직교행렬이 완성되었습니다.
'The Robot > Theory' 카테고리의 다른 글
| [공업수학] 최소자승법 Least Square (28) | 2009/10/11 |
|---|---|
| [공업수학] 행렬의 대각화 (12) | 2009/10/11 |
| [C/C++] 함수 Function 上 (4) | 2009/10/10 |
| [공업수학] 교유값과 고유벡터, 그리고 직교행렬 (24) | 2009/09/28 |
| [C/C++] 반복문 while, do-while, for (6) | 2009/09/27 |
| [공업수학] 역행렬 (Inverse Matrix) (16) | 2009/09/23 |
| [공학입문설계] 팀워크와 팀워크 기술 (14) | 2009/09/16 |
| [공업수학] 행렬식 determinant (4) | 2009/09/14 |
 08 Matrix 04.pdf
08 Matrix 04.pdf

제가 제일 싫어했던 수학이군요. ^^;
선생님이 너무 재미없게 가르쳐 수학은 손도 안댔다는 아픈 기억이...
저런.. 어쩌면 저도 그렇게 재미없는 선생님일까바 걱정되는군요... 좀더 알차게 수업을 꾸며봐야겠습니다^^
공업수학 즐겁게 듣고 있습니다.
수업 프린트 친구에게 부탁하고 직접 프린트 하지 않다가 시험 공부 할려고 들어와 보니, 블로그 상당히 관리를 많이 하시고 계시네요. 굉장히 부지런 하신거 같습니다. 그리고 공수 뿐만 아니라 앞으로의 학교 생활에 필요한 정보들이 많네요.
즐거운 추석 보내시길 바랍니다.
예... 즐거운 추석보내세요..
그리고 저 안부지런합니다..
뻑하면 일찍마치는것만 봐도 알수 있지 않습니까...^^
요즘 한참 다시 하고 있는 행렬과 고유값이네요....
pinkwink님 덕분에 개념정리 새로 하고 있습니다. ^^
헉... 정말 수학공부를 하시는 모양입니다...!!! 우와...
ㅎㅎ 그러니 창피하군요.... 저도 좀더 좋은 자료를 준비해야겠네요^^
저는 그저 통계프로그램 돌리는 것에서 해석할 수 있는 정도만 배우는데도
넘 어렵네요...ㅜㅜ
어려워 보이는데요^^... '그저'라고 말씀하셔도 통계쪽은 한번 우연한 기회에 구경(진짜 구경만....^^)한 적이 있는데, 꽤 아름답게 해석하지 않으면 안되던데요^^ 그저.. 화이팅입니다.^^
헉..수학 너무 어려워요 ㅠㅠ
^^ 저도 어려워서 슬픕니다^^
비밀댓글입니다
ㅎ.. 새로운 행복때문이 아니라 논문작업중이라 생각보다 마음의 여유가 생기질 않네요... 저런저런... ㅎㅎㅎ 그저 다른 분들 블로그에 가서 수다떠는걸로 스트레스 해소중입니다...^^
나름 공업수학은 잘한다 생각했는데 여기 들르니 역시 아직 많이 모자라는걸 느낍니다.
외국서적 번역판이 아닌 교수님이 직접 저술하신 책으로 강의를 듣는데, 없는 내용은 없는데
대신 그만큼 설명이 너무너무 부족하네요. 행렬 norm으로 검색해서 왔다가 케일리-헤밀턴 정리
A^m승 구하기를 배우고 갑니다. 아 여기서 배우고 싶어 ㅠㅠ 잘 보고 갑니다.
부족한 글에 좋은 평가를 내려주셔서 감사합니다.^^
이 글을 읽고 뒷페이지 제일 끝으로 가서 다시 뒤적거렸는데 읽다보니 본글이네요;;
아이젠벡터를 구할때 가우스(아니면 가우스-조르단) 소거법을 사용해서 하는
방법이 있었네요. 저는 배울때 x3 찾고, x2 찾고, x1 찾고 끼워맞춰서 찾으라고
배웠습니다 ㄷ
끼워맞추면 쉬운문제는 답이 바로 나와 좋지만 어렵게 나오면 답이 없더군요.
또 하나 더 배웠네요. 감사합니다.
네... 보통 고유벡터를 찾는게 쪼~~금... 귀찮긴 하지요^^
맨 밑에 있는 루트로 변환되는 거 정말정말 완전 진짜 찾고 있었는데
여기 딱 있었네요 !! 한참찾았는데ㅜㅜ정말 도움 많이 됐습니다
감사합니다 ^.^
예... 감사합니다.^^
궁금한게 있는데 저 람다 123이렇게 정해놨잖아요 그런데 거기에 따라서 또 x123정해지는거구요 근데 123순서를 바껴서 임의로 하면 예로들면
λ1=-4 λ2=0 λ3=3 이렇게 놓으면 값이 달라지지잖아요...그리고 고유값K가 k3을 어떤수로 놓느냐에 따라서도 달라지는데...헷갈리네요ㅠㅠㅠ결국엔 다 같은값을로 치부되는건가....궁금해요
하나의 고유값에 다수의 고유벡터가 있을수있습니다. 그래서 위의 예제에서 다루듯이 고유벡터를 결정하기 위해 한 변수를 가정합니다. 고유값의 순서(??)를 바꾸면 고유벡터도 뭐.. 당연이 그에 맞춰 바꿔야겠지요. 하여간 결론은 고유값에 따라 고유벡터는 다릅니다. 단, 고유값 하나에 고유벡터가 여러개 있을 수 있습니다.
고유 공간은 어떻게 구하는 건가요?
음.. 고유공간? 은 무엇인지 잘 모르겠습니다.
이제 오래되어 기억이 가물가물한 건진 잘 모르겟습니다만..
혹시 영어로 용어를 다시 적어주실 수 있을지요?
영어로는 잘 모르겠고.. 독일어로 Eigenraum이라고 합니다. 고유공간이라는게 이미지가 잘 안떠올라요. 글 올리고 여기저기 기웃거리다가 찾긴했는데. 아주 간단하게 고유벡터가 (1.2.1)t 이면 고유공간은 람다값에 따라 3가지로(람다가 3개면){(1.2.1)}로 표현을 하더라구요. 정확한 뜻을 모르겠어서.. ㅠㅠ 혹시 생각나는게 있으신지요..
아하.. 저런.. 잘모르겠습니다.
(흠.. 배움의길은 끝이 없구요^^)