검색결과 리스트
글
쿼드콥터의 필요성에 대해서는 이전(쿼드콥터 소개...)에 이야기 했었습니다. 이번에는 그 쿼드콥터의 동역학 방정식에 대해서 이야기하겠습니다. 네 개의 로터(f1, f2, f3, f4)를 가진 쿼드콥터는
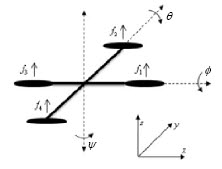
위와 같이 간략화 시킬 수 있습니다. 이 상태에서

전체적으로 작용하는 위치, 병진운동, 회전운동의 에너지 관계식을 위와 같이 만들 수 있는데 이때,
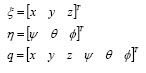
ksi는 병진운동 상태를 eta는 회전운동 상태를 의미하고, q는 그걸 합친 거라고 해 두고 아래의 오일러-라그랑지안 방식으로 유도 하겠습니다.

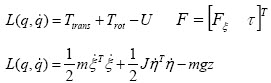
위 식에 각 에너지를 대입하면

와 같이 전개 됩니다.
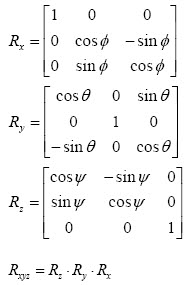
여기서 각 축 중심의 회전행렬로 x-y-z의 3축 회전행렬을 적용하면

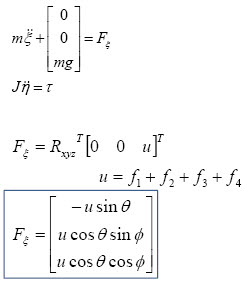
와 같이 제어입력을 정리할 수 있습니다.

여기에 몇몇 인자를 정리하고
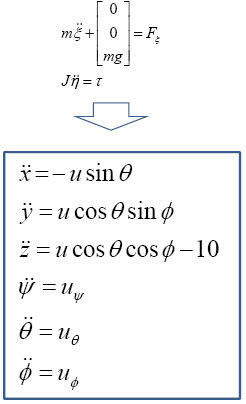
투로터때처럼 시뮬레이션을 위해 파라미터를 좀 가정하면 간단한 쿼드콥터의 동역학 방정식을 얻을 수 있습니다.
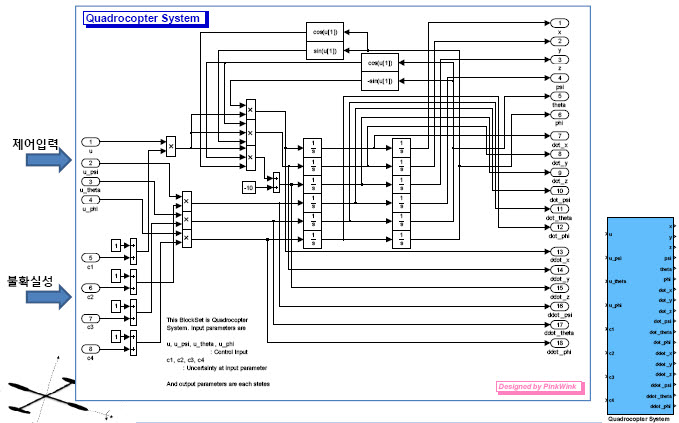
이를 MATLAB/Simulink 블럭으로 꾸며 놨습니다. 역시 c1,c2,c3,c4는 불확실성을 고려한 것이기 때문에, 필요없으면 '0'을 인가하면 됩니다.
| NT-ARSv1 (각도 측정, 자이로 센서 가속도 센서 이용, ARS, IMU) |
자이로 센서와 가속도 센서를 이용한 각도 측정의 어려움을 해결할 수 있는 ARS모듈로 낮은 가격과 작은 크기를 가지며, 금속 케이스가 있어 활용도가 높음. NT-ARSv1 : 관련페이지

'The Robot > ControlTheory' 카테고리의 다른 글
| T-S 퍼지 모델을 이용한 Two-Rotor 시스템의 제어기 설계 (0) | 2009/07/20 |
|---|---|
| T-S 퍼지 모델을 이용한 로터리 펜들럼 제어기 설계 (4) | 2009/07/20 |
| 투로터제어기를 이용한 쿼드콥터 제어기 설계 (10) | 2009/05/31 |
| 쿼드콥터의 궤환선형화기법을 이용한 제어기 설계 (2) | 2009/05/19 |
| 쿼드콥터(Quadcopter)의 동역학 방정식 (16) | 2009/05/19 |
| 궤환선형화 기법을 사용한 Two-Rotor 안정화 제어기 설계 (6) | 2009/05/19 |
| Two-Rotor (VTOL) 시스템의 동역학 모델 (6) | 2009/05/19 |
| 쿼드콥터 소개... (6) | 2009/04/20 |
설정
트랙백
-
Quadcopter
Trackback from Keep It Simple
2010/08/03 23:13
[ DELETE ]
Quadcopter라는 것이 무엇인지 급 궁금해서 검색질 한번. Quadcopter 프로젝트 Quadcopter A new 1000mm Quad Copter Design Quadcopter Prototype ArduIMU quadcopter drone Project Quadcopter Quadcopter 커뮤니티 네이버 quadcopter 자작카페 기술자료 Quadcopter 동역학 방정식 Quadcopter control _ IRS 2009 대회..
 QuadrocopterModel.mdl
QuadrocopterModel.mdl

상당히 늦은 댓글이지만
Rx, Ry, Rz 행렬이 각 축을 중심으로 회전시킨 각도로 인한 벡터 변화를 행렬식 곱으로 보정하기위한 식 같은데 그보다 위에 나온 그림이랑 좀 안맞는거 같은데요(...)
그림에서 x축이랑 z축이 바뀌면 식이랑 맞을거 같네요
근데 그러면 ksi랑 eta 행렬이 안맞으니(...)
네.. 말씀하신데로.. 딴건 다 그대로 두고, 그림에서 x,z축의 글자만 바꾸면 되겠네요.. 어쩌다 실수를 한것인지...ㅠㅠ
감사합니다.^^
혹시 Quadrotor 카페에 양력 테스트한 글을 올리셨던데
그림이 안보여서 죄송한데 자료좀 보내주실 수 있으신가요?
mgy777@nate.com입니다. 감사합니다. ^^
아주 오래전 글이어서... 지금 저도 가지고 있지 않습니다.
뎃글 달아주셔서 감사합니다. 간단하게 설명이라도
해주시면 정말 도움이 될거같습니다. 염치없는 요구인거
같긴한데. ㅠㅠ
당시에는 로드셀을 설치하고, 지렛대처럼 프로펠러가 회전하면 그 로드셀을 누르는 정도를 측정했습니다. 그러나, 프로펠러에서 발생하는 힘을 정말 크게 단순히 해서 1차계로 보더라도, 로드셀에서 읽는 값이 정상상태에서는 믿을 수 있다하더라도, 과도상태에서는 로드셀의 응답속도가 너무 느려 신뢰할 수가 없었습니다. 그래서, 실험을 중단했었습니다. 그 후 쿼드콥터를 계속 진행했다면, 뭔가 성과가 나왔을텐데, 그 후에는 자이로+가속도센서로 자세추정에 주력하다보니....
하여간 위의 이유로 신뢰할 수 없는 데이터라 저도 삭제해버렸답니다.ㅠㅠ
답변 너무 감사합니다.^^
어떻게든 스스로 찾아봐야겠네요.
수고하세요~~
네.. 안타까운일이지만, 이 경우는 직접실험을 하시는게 가장좋을 거라고 생각합니다.^^
안냥하세요
지금 댓글로 질문써도 보실려나,,,
무식한질문 하나 하겠슴니다
상태방정식으로 표현하려면 dot_x=Ax+Bu로 표현될텐데 위식에서는 상태변수가 우변에 안보이내요 A가0인 경우로봐야하나요?
상태방정식이 아니라 동역학을 유도했습니다.
저기서 선형화를 거쳐서 상태방정식을 유도할 수도 있을겁니다.
전 그냥 동역학을 비선형으로 보고 싶었었거든요^^
안녕하세요?
이 동역학에서는 동작점 부근에서 선형화를 한다고 해도 제어입력이 상태변수에 곱해지는 꼴이라, x_dot=Ax+Bu형태로 유도가 안되는 것 같습니다.
제가 제어공학에는 문외한인지라, 선형시불변시스템외에는 다룰 줄 모르는 데요, 강좌에 언급하신 궤환선형화기법이 이런형태의 시스템에 쓰라고 개발된 방법인 것 같습니다. 혹시 궤환선형화기법에 대해 체계적으로 접근하려면 어느 텍스트를 봐야 하는지요? 이 강좌에 언급한 내용만으로는 감을 좀 잡기가 힘드네요.
네 말씀하신대로입니다. 기구부를 약간 바꿔서 선형화할 수 있는 동역학을 얻든지 아니면 저는 궤환선형화나 TS 퍼지를 봤구요. 궤환선형화는 논문으로 익혔습니다.
Nonlinear Control Design for Slightly Non- minimum Phase Systems: Application to V/STOL Aircraft
JOHN HAUSER, SHANKAR SASTRYII and GEORGE M EYER
라는 논문을 저는 봤었습니다. 1992년도 논문이지만, 구글에서 쉽게 찾을 수 있습니다.
이 논문은 한편의 드라마 같은 논문으로 저는 석사때 처음 이 논문을 보고, 이해를 못하고(^^) 다시 보고 또 이해를 못하고(ㅠㅠ) 그러다가 조금씩 이해하면서 이렇게 쓰는 논문도 있구나... 하고 일종의 감명도 받았던 논문이랍니다. ^^
안녕하세요?
소개해 주신 울프럼 알파로 x,y,z 축으로 회전 변환을 해 보니, Fx,Fy 부호가 바뀐 것 같습니다.
암턴...
질문은...
Fy성분에 cos(theta)가 곱해진 것을 보면, Fx성분에도 cos(phi)가 곱해져야 할 것 같은 데요,
직관적으로 봐도 그래야 될 것 처럼 보이고...
회전 변환 행렬을 취해서 결과를 보면 그렇지 않은데, 왜 그런 걸까요?
네.. 안녕하세요 부호는 틀린건지 아닌지는 확인해보지 않았습니다.
회전행렬을 적용하고 나타난 결과라 결과식만 놓고 이야기하기에는 어려움이 있습니다.
예전에 저도 동일한 의문을 가졌던 적이 있었고,
그래서 회전행렬을 적용하지 않고
기하학적으로 풀었을때도(물론 동역학이 아니라 유사환경에서) 회전행렬을 적용한것과 유사했습니다. 그러나 너무 힘들고 복잡해서 나중에는 그게 맞는지도 혼돈이...ㅠㅠ 그래서 회전행렬이라는 것을 쓰나봅니다.
제가 회전 변환 순서를 거꾸로 해서 부호가 반대로 나왔군요, 죄송합니다.
아 그런가요? 아무튼 찾으셨다니 다행입니다.
좋은 성과 있으시길 바랍니다.